Cho hàm số f x = 0 k h i x = π 2 + k π , k ∈ ℤ 1 2 + tan 2 x
Tìm điều kiện của a để hàm số g x = f x + f a x tuần hoàn
A. a ∈ Z
B. a ∈ Q
C. a ∈ N
D. a ∈ 0 ; + ∞
Những câu hỏi liên quan
Cho F(x) là một nguyên hàm của hàm số
f
(
x
)
1
1
+
sin
2
x
với
x
∈
R
{
-
π
4
+
k
π
,
k
∈
}...
Đọc tiếp
Cho F(x) là một nguyên hàm của hàm số f ( x ) = 1 1 + sin 2 x với x ∈ R { - π 4 + k π , k ∈ } . Biết F(0)=1,F( π )=0, tính giá trị biểu thức P = F ( - π 12 ) - F ( 11 π 12 )
Cho K là một khoảng và hàm số yf(x) có đạo hàm trên K. Giả sử f’(x)0 chỉ tại một số hữu hạn điểm trên K. Khẳng định nào sau đây là đúng? A. Nếu
f
x
≥
0
,
∀
x
∈
K
thì hàm số là hàm hằng trên K B. Nếu
f
x
0
,
∀
x
∈
K
thì...
Đọc tiếp
Cho K là một khoảng và hàm số y=f(x) có đạo hàm trên K. Giả sử f’(x)=0 chỉ tại một số hữu hạn điểm trên K. Khẳng định nào sau đây là đúng?
A. Nếu f ' x ≥ 0 , ∀ x ∈ K thì hàm số là hàm hằng trên K
B. Nếu f ' x > 0 , ∀ x ∈ K thì hàm số nghịch biến trên K
C. Nếu f ' x < 0 , ∀ x ∈ K thì hàm số đồng biến trên K
D. Nếu f ' x ≤ 0 , ∀ x ∈ K thì hàm số nghịch biến trên K
Cho K là một khoảng và hàm số yf(x) có đạo hàm trên K. Giả sử f (x)0 chỉ tại một số hữu hạn điểm trên K. Khẳng định nào sau đây là đúng? A. Nếu thì hàm số là hàm hằng trên K. B. Nếu thì hàm số nghịch biến trên K. C. Nếu thì hàm số đồng biến trên K. D. Nếu thì hàm số nghịch biến trên K.
Đọc tiếp
Cho K là một khoảng và hàm số y=f(x) có đạo hàm trên K. Giả sử f '(x)=0 chỉ tại một số hữu hạn điểm trên K. Khẳng định nào sau đây là đúng?
A. Nếu 
thì hàm số là hàm hằng trên K.
B. Nếu 
thì hàm số nghịch biến trên K.
C. Nếu 
thì hàm số đồng biến trên K.
D. Nếu 
thì hàm số nghịch biến trên K.
Bài 1: Cho hàm số Y= f(x)=k.x ( k là hằng số , k khác 0). Chứng minh rằng:
a, f(10x) =10.f(x)
b, f(x1 + x2 ) = f(x1) + f(x2)
Bài 2: cho các hàm số y=2x và y= \(\frac{18}{x}\)không vẽ đồ thị . Tìm tọa độ giao điểm của hàm số đã cho.
Bài 1: Cho hàm số Y= f(x)=k.x ( k là hằng số , k khác 0). Chứng minh rằng:
Giải thích các bước:
a)f(10x) = 10f(x)
ta có:
y= f (x) =kx
=>f(10x) = k(10x) =10kx (*)
=>10f(x) = 10kx (**)
Từ (*) và (**)
=> f(10x) =10f(x)
=>đpcm
b)
f(x1 - x2) = k.(x1 - x2) (1)
f(x1) - f(x2) = k.x1 - k.x2 = k.(x1 - x2) (2)
Từ (1) và (2) => đpcm
Giải thích các bước:
a)f(10x) = 10f(x)
ta có:
y= f (x) =kx
=>f(10x) = k(10x) =10kx (*)
=>10f(x) = 10kx (**)
Từ (*) và (**)
=> f(10x) =10f(x)
=>đpcm
b)
f(x1 - x2) = k.(x1 - x2) (1)
f(x1) - f(x2) = k.x1 - k.x2 = k.(x1 - x2) (2)
Từ (1) và (2) => đpcm
Hàm số f(x) có đạo hàm f’(x) trên khoảng K. Cho đồ thị của hàm số f’(x) trên khoảng K như sau:
Số điểm cực trị của hàm số f(x) trên K là:
A. 1
B.2
C. 3
D. 4
Dựa vào đồ thị ta thấy phương trình 
chỉ có một nghiệm đơn và hai nghiệm kép nên 
chỉ đổi dấu khi qua nghiệm đơn này.
Do đó suy ra hàm số f(x) có đúng một cực trị.
Chọn A.
Đúng 0
Bình luận (0)
cho hàm số y= f(x)=kx(k là hằng số khác 0 ) ta có f(10x)=
cho hàm số y=f(x)=kx(k là hằng số và khác 0)cmr: f(x1-x2)=f(x1)-f(x2)
Hàm số f(x) có đạo hàm f’(x) trên khoảng K. Cho đồ thị của hàm số f’(x) trên khoảng K như sau: Số điểm cực trị của hàm số trên K là: A .1 B. 2 C. 3 D. 4
Đọc tiếp
Hàm số f(x) có đạo hàm f’(x) trên khoảng K. Cho đồ thị của hàm số f’(x) trên khoảng K như sau:
Số điểm cực trị của hàm số 
trên K là:
A .1
B. 2
C. 3
D. 4
Dựa vào đồ thị ta thấy phương trình 
có ba nghiệm đơn và 
đổi dấu khi qua nghiệm đơn này.
Do đó suy ra hàm số 
có ba điểm cực trị.
Chọn C.
Đúng 0
Bình luận (0)
Cho hàm số y = f(x) = kx (k là hằng số, k ( 0). Chứng minh rằng:
a/ f(10x) = 10f(x)
b/ f(x1 + x2) = f(x1) + f(x2)
c/ f(x1 - x2) = f(x1) - f(x2)
Cho khoảng K,
x
0
∈
K
và hàm số y f(x) xác định trên
K
x
0
Chứng minh rằng nếu
lim
x
→
x
0
f
(
x
)
+
∞
t...
Đọc tiếp
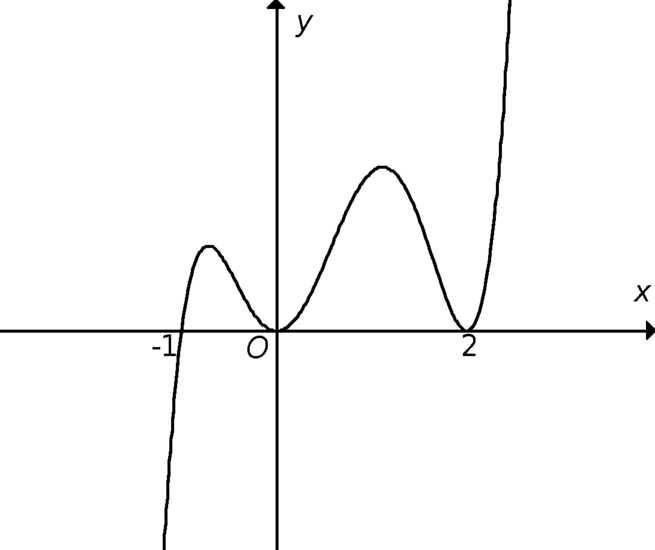
Cho khoảng K, x 0 ∈ K và hàm số y = f(x) xác định trên K \ x 0
Chứng minh rằng nếu lim x → x 0 f ( x ) = + ∞ thì luôn tồn tại ít nhất một số c thuộc sao cho f(c) > 0
Vì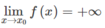 
nên với dãy số ( x n ) bất kì, x n ∈ K \ x 0 và x n → x 0 ta luôn có
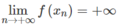
Từ định nghĩa suy ra f ( x n ) có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi.
Nếu số dương này là 1 thì f ( x n ) > 1 kể từ một số hạng nàođó trởđi.
Nói cách khác, luôn tồn tạiít nhất một số x k ∈ K \ x 0 sao cho f ( x k ) > 1 .
Đúng 0
Bình luận (0)