Cho các điểm A (-2,m), B (-6;m) và C (-6;-4). Trong đó m là 3 a, Tìm D sao cho ABCD là hình bình hành b, Tính các góc của ABCD

Những câu hỏi liên quan
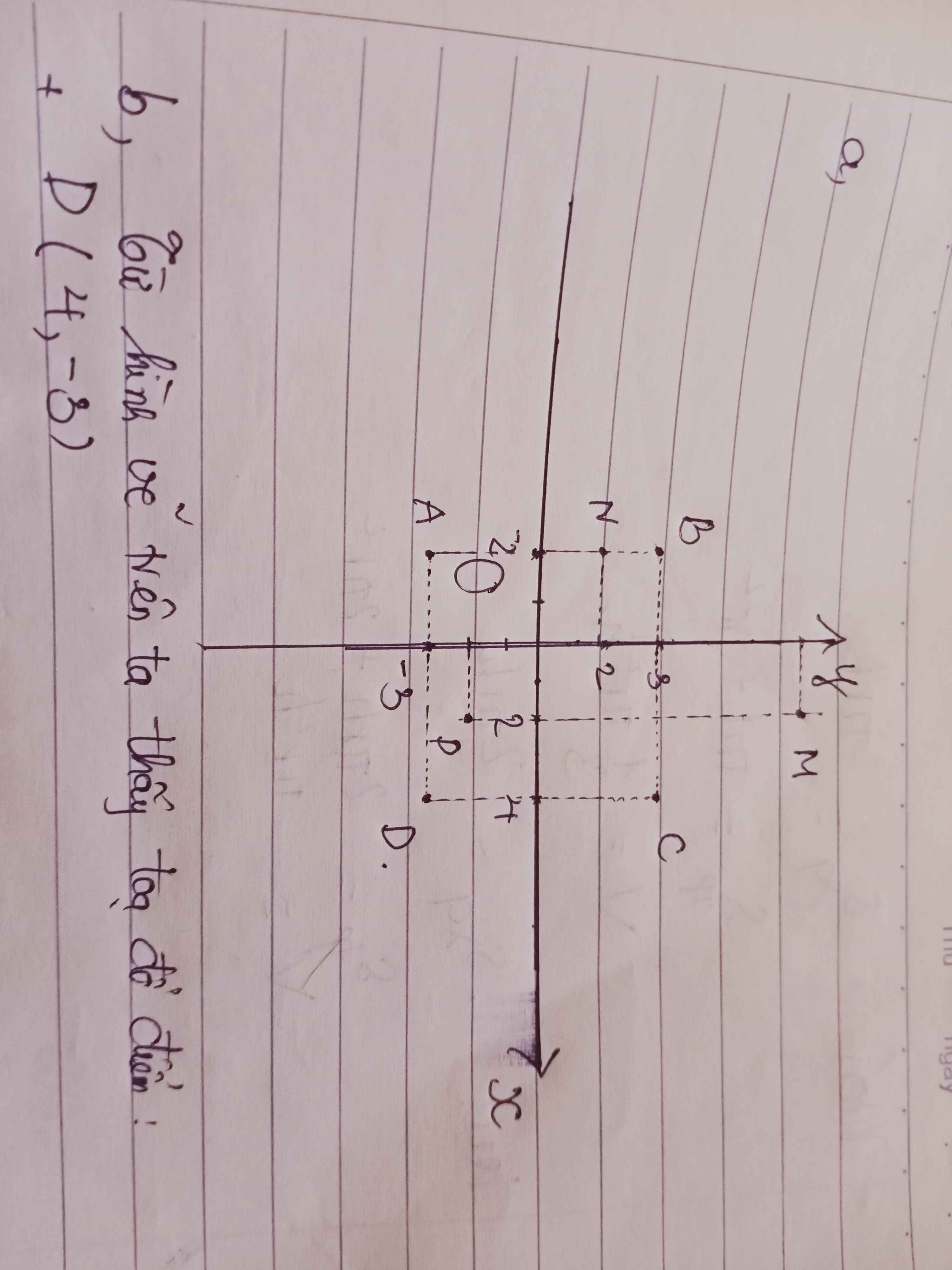
Cho các điểm sau: A(–2; –3); B(–2; 3); C(4; 3); M(2; 6); N(–2; 2); P(2; –2).
a) Biểu diễn các điểm đã cho trên mặt phẳng tọa độ.
b) Tìm tọa độ điểm D; Q sao cho ABCD và MNPQ là hình vuông.
Cho các điểm sau: A(–2; –3); B(–2; 3); C(4; 3); M(2; 6); N(–2; 2); P(2; –2).
a) Biểu diễn các điểm đã cho trên mặt phẳng tọa độ.
b) Tìm tọa độ điểm D; Q sao cho ABCD và MNPQ là hình vuông.
Cho các điểm sau: A(–2; –3); B(–2; 3); C(4; 3); M(2; 6); N(–2; 2); P(2; –2).
a) Biểu diễn các điểm đã cho trên mặt phẳng tọa độ.
b) Tìm tọa độ điểm D; Q sao cho ABCD và MNPQ là hình vuông.
cho 4 điểm M ,N ,P ,Q sao cho : điểm N nằm giữa 2 điểm M và P ; ba điểm M, N, Q không thẳng hàng . Số các đường thẳng phân biệt đi qua ít nhất hai điểm đã cho là ?
A .3 B.4 C.5 D.6
cho hàm số y = -2 .x
a) cho điểm e ( -6; m ) thuộc đồ thị hàm số . tìm m
b) cho các điểm a ( -1/2 ; 1 ) và ( 2;-4) trên mặt phẳng tọa độ . chứng minh rằng các điểm a,o,b thẳng hàng .
giải giùm mình nhé
Trong mặt phẳng toạ độ Oxy, cho tam giác ABC. Các điểm M(1;- 2), N(4;- 1) và P(6 ; 2) lần lượt là trung điểm của các cạnh BC, CA, AB. Tìm toạ độ của các điểm A, B, C.
Theo tích chất đường trung bình trong một tam giác ta có: \(\overrightarrow {PN} = \overrightarrow {BM} = \overrightarrow {MC} \) và \(\overrightarrow {MP} = \overrightarrow {NA} \)
Gọi \(A\left( {{a_1},{a_2}} \right),B\left( {{b_1};{b_2}} \right),C\left( {{c_1};{c_2}} \right)\)
Ta có: \(\overrightarrow {PN} = \left( {2;3} \right)\),\(\overrightarrow {BM} = \left( {1 - {b_1}; - 2 - {b_2}} \right)\), \(\overrightarrow {MC} = \left( {{c_1} - 1;{c_2} + 2} \right)\), \(\overrightarrow {MP} = \left( {5;4} \right)\), \(\overrightarrow {NA} = \left( {{a_1} - 4;{a_2} + 1} \right)\)
Có \(\overrightarrow {PN} = \overrightarrow {BM} \Leftrightarrow \left\{ \begin{array}{l}2 = 1 - {b_1}\\3 = - 2 - {b_2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{b_1} = - 1\\{b_2} = - 5\end{array} \right.\) .Vậy \(B\left( { - 1; - 5} \right)\)
Có \(\overrightarrow {PN} = \overrightarrow {MC} \Leftrightarrow \left\{ \begin{array}{l}2 = {c_1} - 1\\3 = {c_2} + 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{c_1} = 3\\{c_2} = 1\end{array} \right.\) .Vậy \(C\left( {3;1} \right)\)
Có \(\overrightarrow {NA} = \overrightarrow {MP} \Leftrightarrow \left\{ \begin{array}{l}5 = {a_1} - 4\\4 = {a_2} + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{a_1} = 9\\{a_2} = 3\end{array} \right.\) .Vậy \(A\left( {9;3} \right)\)
Đúng 0
Bình luận (0)
bài 1:Cho tập hợp M {5; 8; 9; 1986; 2010}. Có bao nhiêu tập hợp con của M gồm những số chẵnbài 2:Cho hai tập hợp A {1; 2; 3; 4; 5; 6} và B là tập hợp các số tự nhiên lẻ, lớn hơn 2. Gọi C là một tập hợp con nào đó của cả hai tập hợp A và B. Số phần tử nhiều nhất có thể của C làbài 3 :Cho 6 điểm trong đó không có 3 điểm nào thẳng hàng. Số tất cả các đường thẳng đi qua 2 trong 6 điểm đã cho làbài 4 :Cho 6 điểm trong đó không có 3 điểm nào thẳng hàng. Số tất cả các tam giác có 3 đỉnh là 3 trong 6...
Đọc tiếp
bài 1:Cho tập hợp M = {5; 8; 9; 1986; 2010}. Có bao nhiêu tập hợp con của M gồm những số chẵn
bài 2:Cho hai tập hợp A = {1; 2; 3; 4; 5; 6} và B là tập hợp các số tự nhiên lẻ, lớn hơn 2. Gọi C là một tập hợp con nào đó của cả hai tập hợp A và B. Số phần tử nhiều nhất có thể của C là
bài 3 :Cho 6 điểm trong đó không có 3 điểm nào thẳng hàng. Số tất cả các đường thẳng đi qua 2 trong 6 điểm đã cho là
bài 4 :Cho 6 điểm trong đó không có 3 điểm nào thẳng hàng. Số tất cả các tam giác có 3 đỉnh là 3 trong 6 điểm đã cho là:
nếu làm được thì mình tick cái nha>-
Bài 6: Cho hàm số y=f(x)=ax
a) Xác định a biết đths đi qua điểm A (2; 5)
b) Các điểm M(1; 3), N(4; 10) có thuộc đths không?
a, đths đi qua A(2;5) <=> 5 = 2a <=> a = 5/2
b, đề bạn có thiếu ko ?
Đúng 0
Bình luận (1)
Cho A(1;2) ; B( -2; 6). Điểm M trên trục Oy sao cho ba điểm A; B; M thẳng hàng thì tọa độ điểm M là:
A.(0; -10)
B. (0; 10)
C.( 0; 5)
D.( -10; 0)
Cho A(1;2) ; B( -2; 6). Điểm M trên trục Oy sao cho ba điểm A; B; M thẳng hàng thì tọa độ điểm M là:
A.(0; -10)
B. (0; 10)
C.( 0; 5)
D.( -10; 0)
Chọn B.
Ta có M nằm trên trục Oy nên tọa độ điểm M có dạng M(0; y)
Ba điểm A; B; M thẳng hàng khi ![]() cùng phương với
cùng phương với ![]()
Ta có ![]() . Do đó,
. Do đó, ![]() cùng phương với
cùng phương với
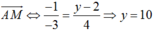
Vậy M(0; 10) .
Đúng 0
Bình luận (0)