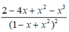Xét tính chẵn lẻ của hàm số y = f x = 1 - 2 x + 2 x + 1 ta có
A. f(x) là hàm số lẻ.
B. f(x) là hàm số chẵn.
C. f(x) là hàm số không chẵn, không lẻ.
D. f(x) là hàm số vừa chẵn vừa lẻ.
Xét tính chẵn lẻ của hàm số sau
Y=|X-1| / |x-1|-2
\(\frac{ }{ }\)
Hãy rút ra nhận xét về dấu của lũy thừa vs số mũ chẵn và lũy thừa vs số mũ lẻ của 1 số hữu tỉ âm
Lũy thừa với số mũ chẵn của một số âm là một số dương
Lũy thừa với số mũ lẻ của mọt số âm là một số âm
Bài 1: xét tính liên tục của hàm số
g(x)=\(\left\{{}\begin{matrix}\dfrac{x^2-3x+2}{x^3-8}khix< 2\\x+1khix\ge2\end{matrix}\right.\)tại x0=2
Bài 2: Tìm a để hàm số sau liên tục trên R:
g(x)= \(\left\{{}\begin{matrix}\dfrac{\sqrt{3x-2}-2}{x-2}khix>2\\ax-1khix\le2\end{matrix}\right.\)tại x0=2
1/ \(\lim\limits_{x\rightarrow2^+}f\left(x\right)=\lim\limits_{x\rightarrow2^+}\left(x+1\right)=f\left(2\right)=3\)
\(\lim\limits_{x\rightarrow2^-}f\left(x\right)=\lim\limits_{x\rightarrow2^-}\dfrac{\left(x-2\right)\left(x-1\right)}{\left(x-2\right)\left(x^2+2x+4\right)}=\lim\limits_{x\rightarrow2^-}\dfrac{x-1}{x^2+2x+4}=\dfrac{1}{12}\)
\(\lim\limits_{x\rightarrow2^+}f\left(x\right)=f\left(2\right)\ne\lim\limits_{x\rightarrow2^-}f\left(x\right)\)
=> ham so gian doan tai x=2
2/ \(\lim\limits_{x\rightarrow2^-}f\left(x\right)=f\left(2\right)=2a-1\)
\(\lim\limits_{x\rightarrow2^+}f\left(x\right)=\lim\limits_{x\rightarrow2^+}\dfrac{3x-2-4}{\left(x-2\right)\left(\sqrt{3x-2}+2\right)}=\lim\limits_{x\rightarrow2^+}\dfrac{3}{\sqrt{3x-2}+2}=\dfrac{3}{4}\)
De ham so lien tuc tai x=2
\(\Leftrightarrow\lim\limits_{x\rightarrow2^-}f\left(x\right)=f\left(2\right)=\lim\limits_{x\rightarrow2^+}f\left(x\right)\Leftrightarrow2a-1=\dfrac{3}{4}\Leftrightarrow a=\dfrac{7}{8}\)
Cho hàm số y=f(x) có đạo hàm trên R. Đường cong trong hình vẽ bên là đồ thị của hàm số y=f’(x),(y=f’(x) liên tục trên R). Xét hàm số g x = f x 2 - 2 . Mệnh đề nào dưới đây sai?
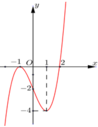
A. Hàm số g(x) nghịch biến trên (-∞;-2).
B. Hàm số g(x) đồng biến trên (2;+∞).
C. Hàm số g(x)nghịch biến trên(-1;0).
D. Hàm số g(x) nghịch biến trên (0;2).
Bài 1: Cho hàm số y = f(x) = 5 - 2x
a) Tính f(-2); f(-1)
b) Tính các giá trị của x ứng với các giá trị của y lần lượt là 5; 3; -1
Bài 2: Tìm tập xác định của các hàm số sau:
a) y = x3 - 2x2 + x -1
b) y = \(\sqrt{2x-1}\)
c) y = \(\frac{x-1}{\left(x+1\right)\left(x-3\right)}\)
Tính đạo hàm của hàm số sau: y = (x2 – x + 1)3.(x2 + x + 1)2
A: (x2 – x + 1)2(x2 + x + 1)
B: (x2 – x + 1)2(x2 + x + 1)[(2x + 3)(x + x2)]
C: (x2 – x + 1)2(x2 + x + 1)[3(2x - 1) + 2(2x + 1)]
D: Tất cả sai
Chọn D.
Đầu tiên sử dụng quy tắc nhân.
y’ = [(x2 – x + 1)]’(x2 + x + 1)2 + [(x2 x + 1)2]/(x2 – x + 1)3.
Sau đó sử dụng công thức u a '
y' = 3(x2 – x + 1)2(x2 – x + 1)’(x2 + x + 1) + 2(x2 + x + 1)(x2 + x + 1)’(x2 – x + 1)3
y’ = 3(x2 – x + 1)2(2x – 1) (x2 + x + 1)2 + 2(x2 + x + 1)(2x + 1)(x2 – x + 1)3
y’ = (x2 – x + 1)2(x2 + x + 1)[3(2x – 1)(x2 + x + 1) + 2(2x + 1)(x2 – x + 1)].
Tính đạo hàm của hàm số sau y = x(2x - 1)(3x + 2)
A: 18x2 + 2x + 2
B: 18x2 + 2x - 2
C: 9x2 + 2x - 2
D: 2x - 2
Chọn B.
Ta có: y = (2x – 1)(3x + 2) = (2x2 – x)(3x + 2)
y’ = [(2x2 – x)(3x + 2)]’ = (2x2 – x)’(3x + 2) + (3x + 2)’.(2x2 – x)
= (4x – 1)(3x + 2) + 3(2x2 – x) = 18x2 + 2x – 2.
Cho dãy A gồm N số nguyên dương A1,A2,A3...An (N<=500).Viết chương trình thực hiện tính tổng các số lẻ của dãy. Viết hàm kiem_tra (x:integer):boolean;(hàm trả về giá trị bằng TRUE nếu x là số lẻ, hàm trả về giá trị bằng FALSE nếu x là số chẵn
uses crt;
var a:array[1..500]of integer;
i,n,t:integer;
{----------------------chuong-trinh-con------------------------}
function kiem_tra(x:integer):boolean;
begin
if x mod 2<>0 then kiem_tra:=true
else kiem_tra:=false;
end;
{----------------------chuong-trinh-chinh----------------------}
begin
clrscr;
repeat
write('Nhap n='); readln(n);
until (0<n) and (n<=500);
for i:=1 to n do
begin
repeat
write('A[',i,']='); readln(a[i]);
until a[i]>0;
end;
t:=0;
for i:=1 to n do
if kiem_tra(a[i])=true then t:=t+a[i];
writeln('Tong cac so le la: ',t);
readln;
end.
Tính đạo hàm của hàm số sau y = 1 + x - x 2 1 - x + x 2
A. 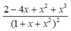
B. 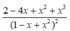
C. 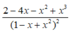
D.