Cho đường thẳng d : y = 3 x - 1 2 . Giao điểm của với trục tung là:
A. A 1 6 ; 0
B. B 0 ; 1 2
C. C 0 ; - 1 6
D. D 0 ; - 1 2
1/ Vẽ đồ thị hàm số (d): y = -x+1 trên hệ trục toạ độ.
2/ Gọi A, B là giao điểm của đường thẳng (d) với các trục ox, oy. Tính diện tích tam giác OAB.
3/ Viết phương trình đường thẳng (d’) song song với đường thẳng (d) và có tung độ góc là -2.
2: Tọa độ điểm A là:
\(\left\{{}\begin{matrix}y_A=0\\-x_A+1=0\end{matrix}\right.\Leftrightarrow A\left(1;0\right)\)
Tọa độ điểm B là:
\(\left\{{}\begin{matrix}x_B=0\\y_B=-0+1=1\end{matrix}\right.\)
Vậy: B(0;1)
\(S_{OAB}=\dfrac{OA\cdot OB}{2}=\dfrac{1}{2}\)
3: Vì (d')//(d) nên a=-1
Vậy: (d'): y=-x+b
Thay x=0 và y=-2 vào (d'), ta được:
b-0=-2
hay b=-2
Cho đường thẳng d : y = ax + b với a,b là hằng số. Tìm a,b biết d song song đường thẳng d2 : y = (-1/3)x + 2017 và đi qua giao điểm của d3 : y = x - 2 với trục tung
Cho hai đường thẳng: (d1):y=1/2x+2 và (d2):y=-x+2
a) vẽ (d1) và (d2) trên cùng một hệ trục toạ độ Oxy
b) gọi A là giao điểm của (d1) với trục hoành. Tìm toạ độ điểm A
c) gọi B là giao điểm của (d2) với trục tung. Tìm toạ đồ điểm B
d)gọi C là giao điểm của (d1) và (d2). Tìm toạ độ điểm C
Mông các bạn giải giúp mình gấp với ạ :3
a/ bạn tự làm
b/ \(\Rightarrow y=0\Rightarrow\dfrac{1}{2}x+2=0\) giải PT tìm hoành độ x
c/ \(\Rightarrow x=0\Rightarrow y=0+2=2\)
d/ \(\Rightarrow\dfrac{1}{2}x+2=-x+2\) Giải PT tìm hoành độ x của C rồi thay vào d1 hoặc d2 để tìm tung độ y của C
Cho (d):y=-x+2 vaà (d'):y=2x-4
1. Vẽ 2 đường thẳng trên cùng 1 mặt phẳng tọa độ
2. Gọi B là giao điểm của (d) với trục trung, C là giao điểm của (d') với trục tung. Tính diện tích tam giác ABC
1: 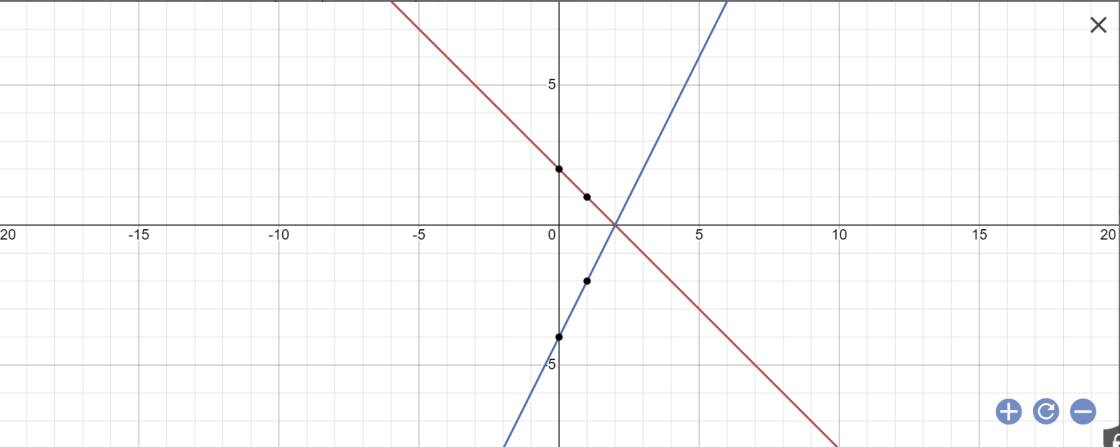
2:Sửa đề: Gọi A là giao điểm của (d) với (d')
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=-x+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=0\\y=-0+2=2\end{matrix}\right.\)
Tọa độ C là
\(\left\{{}\begin{matrix}x=0\\y=2\cdot x-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=2\cdot0-4=-4\end{matrix}\right.\)
Vậy: C(0;-4); B(0;2)
Tọa độ A là:
\(\left\{{}\begin{matrix}-x+2=2x-4\\y=2x-4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-3x=-6\\y=2x-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=2\cdot2-4=0\end{matrix}\right.\)
Vậy: A(2;0)
A(2;0); B(0;2) C(0;-4)
\(AB=\sqrt{\left(0-2\right)^2+\left(2-0\right)^2}=\sqrt{2^2+2^2}=\sqrt{8}=2\sqrt{2}\)
\(AC=\sqrt{\left(0-2\right)^2+\left(-4-0\right)^2}=\sqrt{2^2+4^2}=2\sqrt{5}\)
\(BC=\sqrt{\left(0-0\right)^2+\left(-4-2\right)^2}=6\)
Xét ΔABC có
\(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}\)
\(=\dfrac{8+20-36}{2\cdot2\sqrt{2}\cdot2\sqrt{5}}=\dfrac{-\sqrt{10}}{10}\)
=>\(sinBAC=\sqrt{1-cos^2BAC}=\sqrt{1-\dfrac{1}{10}}=\sqrt{\dfrac{9}{10}}=\dfrac{3}{\sqrt{10}}\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinBAC\)
\(=\dfrac{1}{2}\cdot2\sqrt{2}\cdot2\sqrt{5}\cdot\dfrac{3}{\sqrt{10}}=6\)
viết phương trình đường thẳng
a) đường thẳng song song vs đường thẳng (d1): y=3x-1 và đi qua giao điểm của 2 đường thẳng (d2): y=-x+5 và (d3): y=x-4
b)đường thẳng vuông góc vs đường thẳng (d1) y=-5x-3 và ik qua giao điểm 2 đường thẳng (d2) y=2-3x , (d3) y=-x+4
c)đưởng thẳng cắt trục hoành tại điểm có hoành độ =-1 và song song vs đưởng thẳng y=5x-2
d) đưởng thẳng giao vs trục tung tại điểm D có tung độ =-6 và vuông góc vs đưởng thẳng y=4x+3
e) đường thẳng cắt trục Ox tại điểm E có hoành độ =2 và vuông góc vs đường thẳng y=3x-1
f) biết tung độ giao điểm đường thẳng vs trục Oy =-5 và vuông góc vs đường thẳng y=-2x+3
g) biết hoành độ giao điểm của đường thẳng vs trục Ox =3 và hợp vs Ox 1 góc 30 độ
h) biết tung độ giao điểm đường thẳng vs trục Oy = \(\frac{-1}{2}\) và hợp vs trục Ox 1 góc 60 độ
AI ĐÓ TỐT BỤNG GIÚP MK VS MAI MK KTRA RÙI!!!
bài 1: cho 3 đường thẳng
(d1): y=1/2 x-3; (d2): y= 3-2x ; (d3): y= -7/6 x+1
a, vẽ 3 đườn thẳng trên cùng 1 hệ trục tọa độ. chứng minh 3 đường thẳng này đồng quy
b, gọi điểm đồng quy là A. tính chu vi và diện tích có đỉnh A, 2 điểm còn lại là giao điểm của (d1) và (d2) với trục tung
Bài 1. Cho hai đưong thẳng có phương trình là: y=-2x+3 (dı) và y=0,5x-2 (d:).
a) Tim tọa độ giao điểm C của (di) và (d2).
b) Gọi A, B lần lượt là giao điểm của đường thẳng (di) và (dz) với trục tung. Tinh diện tích tam giác ABC.
a: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}-2x+3=0,5x-2\\y=-2x+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=-1\end{matrix}\right.\)
b: Tọa độ điểm A là:
\(\left\{{}\begin{matrix}x=0\\y=-2\cdot0+3=3\end{matrix}\right.\)
Tọa độ điểm B là:
\(\left\{{}\begin{matrix}x=0\\y=0.5\cdot0-2=-2\end{matrix}\right.\)
Vậy: A(0;3); B(0;-2); C(2;-1)
\(AB=\sqrt{\left(0-0\right)^2+\left(-2-3\right)^2}=5\)
\(AC=\sqrt{\left(2-0\right)^2+\left(-1-3\right)^2}=2\sqrt{5}\)
\(BC=\sqrt{\left(2-0\right)^2+\left(-1+2\right)^2}=\sqrt{5}\)
Vì \(AC^2+BC^2=AB^2\) nên ΔABC vuông tại C
\(S_{BAC}=\dfrac{AC\cdot BC}{2}=\dfrac{2\sqrt{5}\cdot\sqrt{5}}{2}=5\left(đvdt\right)\)
a. -2x+3=0,5x-2
2,5x = 5
=> x= 2
=> y = -1
Vậy C ( 2;-1 ) là giao điểm của (di ) (dz )
1. Cho 2 hàm số y = 2x + 2 (1) và y = -\(\frac{1}{2}\)x - 2 (2)
a) Gọi giao điểm của các đường thẳng có PT (1) và (2) với trục Ox lần lượt tại A và B. Giao điểm của 2 đường thẳng đó là C. Tính diện tích và chu vi của tam giác ABC
b) Tính góc tạo bởi đường thẳng (1) và (2) với trục Ox
2. Cho hàm số y = (m - 1)x + m + 2 (3)
2.1. Tìm m để ĐTHS (3) là đường thẳng:
a) Cắt trục tung tại điểm có tung độ bằng 1 - \(\sqrt{2}\)
b) Cắt trục hoành tại điểm có hoành độ bằng 2 + \(\sqrt{2}\)
c) Cắt đường thẳng y = 2x - 3 tại 1 điểm có hoành độ là 1
d) Tạo với trục Ox 1 góc = \(45^o\)
e) Đồng quy với các đường thẳng y = 2x + 1 và y = 4x - 5
f) CM rằng ĐTHS (3) là đường thẳng luôn đi qua 1 điểm cố định với mọi giá trị của m
3. Viết PT đường thẳng (d) biết rằng đường thẳng (d):
a) Đi qua 2 điểm A(-1;2) và // với đường thẳng y = 3x - 2
b) Cắt trục tung tại điểm có tung độ = 1 và cắt trục hoành tại điểm có hoành độ = 3
c) Cắt đường thẳng -2y + x - 3 = 0 tại 1 điểm nằm trên trục tung.
~ GIÚP MÌNH VỚI!! GẤP!
~ MÌnh cảm ơn nhiều!
1/ Cho đường thẳng (d): y=2x+m+1. Tìm các giá trị của m để đường thẳng (d) cắt trục tung và trục hoành tại A và B sao cho diện tích tam giác OAB bằng 9 (đvdt).
2/ Cho parabol (P): y=x^2
và đường thẳng (d) có hệ số góc là a khác 0 đi qua điểm M(1;2)
a/ Cm rằng (d) luôn luôn cắt P tại hai điểm phân biệt với mọi a khác 0.
b/ Gọi xA và xB là hoành độ giao điểm của P và d. Chứng minh rằng xA+xB-xA.xB=2.
3/ Cho đường thẳng d: (m+1)x + (m-3)y=1
a/ Chứng minh đường thẳng d luôn đi qua một điểm với mọi m và tìm điểm cố định đó.
b/ Gọi h là khoảng cách từ O đến đường thẳng d. Tìm các giá trị của m để h lớn nhất.
Bài 2: Cho hai đường thẳng y = 2x –1 ![]() và y = – x + 2
và y = – x + 2 ![]()
a) Tìm tọa độ giao điểm M của ![]() và
và ![]() .
.
b) Viết phương trình đường thẳng (d) qua M và cắt trục tung tại điểm có tung độ bằng 4.
c) Viết phương trình đường thẳng ![]() qua gốc tọa độ và song song với
qua gốc tọa độ và song song với ![]() .
.
\(a,PTHDGD:2x-1=-x+2\Leftrightarrow x=1\Leftrightarrow y=1\Leftrightarrow M\left(1;1\right)\\ b,\text{Gọi đt của }\left(d\right)\text{ là }y=ax+b\left(a\ne0\right)\\ \Leftrightarrow\left\{{}\begin{matrix}a+b=1\\0a+b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-3\\b=4\end{matrix}\right.\Leftrightarrow\left(d\right):y=-3x+4\)