1: 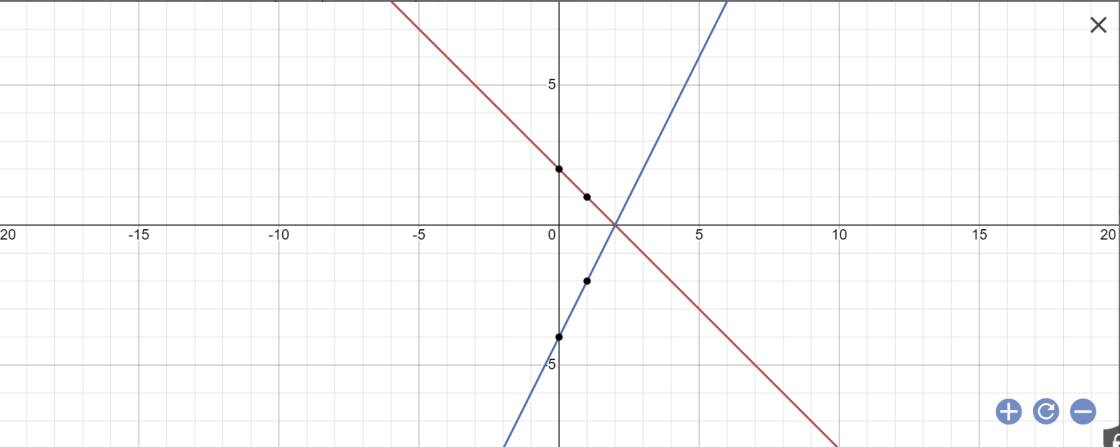
2:Sửa đề: Gọi A là giao điểm của (d) với (d')
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=-x+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=0\\y=-0+2=2\end{matrix}\right.\)
Tọa độ C là
\(\left\{{}\begin{matrix}x=0\\y=2\cdot x-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=2\cdot0-4=-4\end{matrix}\right.\)
Vậy: C(0;-4); B(0;2)
Tọa độ A là:
\(\left\{{}\begin{matrix}-x+2=2x-4\\y=2x-4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-3x=-6\\y=2x-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=2\cdot2-4=0\end{matrix}\right.\)
Vậy: A(2;0)
A(2;0); B(0;2) C(0;-4)
\(AB=\sqrt{\left(0-2\right)^2+\left(2-0\right)^2}=\sqrt{2^2+2^2}=\sqrt{8}=2\sqrt{2}\)
\(AC=\sqrt{\left(0-2\right)^2+\left(-4-0\right)^2}=\sqrt{2^2+4^2}=2\sqrt{5}\)
\(BC=\sqrt{\left(0-0\right)^2+\left(-4-2\right)^2}=6\)
Xét ΔABC có
\(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}\)
\(=\dfrac{8+20-36}{2\cdot2\sqrt{2}\cdot2\sqrt{5}}=\dfrac{-\sqrt{10}}{10}\)
=>\(sinBAC=\sqrt{1-cos^2BAC}=\sqrt{1-\dfrac{1}{10}}=\sqrt{\dfrac{9}{10}}=\dfrac{3}{\sqrt{10}}\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinBAC\)
\(=\dfrac{1}{2}\cdot2\sqrt{2}\cdot2\sqrt{5}\cdot\dfrac{3}{\sqrt{10}}=6\)











