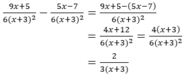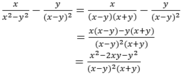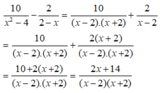Làm phép trừ các phân thức: 10 x 2 - 4 - 2 2 - x .
Những câu hỏi liên quan
SGK Kết nối tri thức và cuộc sống
22 tháng 7 2023 lúc 9:21
Thực hiện các phép cộng, trừ phân thức sau:
a) \(\dfrac{a}{{a - 3}} - \dfrac{3}{{a + 3}}\) b) \(\dfrac{1}{{2x}} + \dfrac{2}{{{x^2}}}\) c) \(\dfrac{4}{{{x^2} - 1}} - \dfrac{2}{{{x^2} + x}}\)
`a, a/(a-3) - 3/(a+3) = (a(a+3) - 3(a-3))/(a^2-9)`
`= (a^2+9)/(a^2-9)`
`b, 1/(2x) + 2/x^2 = x/(2x^2) + 4/(2x^2) = (x+4)/(2x^2)`
`c, 4/(x^2-1) - 2/(x^2+x) = (4x)/(x(x-1)(x+1)) - (2(x-1))/(x(x+1)(x-1))`
`= (2x+2)/(x(x-1)(x+1)`
`= 2/(x(x-1))`
Đúng 1
Bình luận (0)
Thực hiện phép trừ phân thức đại số 2/x-4-2x-6/x-4
\(=\dfrac{2-2x+6}{x-4}=\dfrac{-2x+8}{x-4}=-2\)
Đúng 1
Bình luận (0)
a)Phân tích đa thức thành nhân tử: x ²+x ³-4x+4
b)Thực hiện phép trừ phân thức: 3/2x+6 - x-6/2^2+6x
a, x2+x3-4x+4=x2(x+1)-4(x+1)=(x+1)(x2-4)=(x+1)(x-2)(x+2)
Làm tính trừ các phân thức: 4 x + 7 x 2 + 2 - x + 6 x 2 + 2
Làm tính trừ các phân thức:
9
x
+
5
6
(
x
+
3
)
2
-
5
x
-
7
6
(
x
+
3...
Đọc tiếp
Làm tính trừ các phân thức: 9 x + 5 6 ( x + 3 ) 2 - 5 x - 7 6 ( x + 3 ) 2
Làm tính trừ các phân thức: x x 2 - y 2 - y ( x - y ) 2
Trong các biểu thức đại số sau, biểu thức nào không chứa phép tính cộng, phép tính trừ?
\(3{x^2}\); 6 – 2y ; 3t; \(3{t^2} - 4t + 5\); -7
\(3{u^4} + 4{u^2}\); \( - 2{z^4}\); 1; \(2021{y^2}\)
Các biểu thức không chứa phép cộng, phép trừ là : \(3{x^2};3t; - 7; - 2{z^4};1;2021{y^2}\)
Đúng 0
Bình luận (0)
Thực hiện phép trừ các phân thức:
10
x
2
-
4
-
2
2
-
x
. A.
2
x
+
14
(
x
-
2
)
(...
Đọc tiếp
Thực hiện phép trừ các phân thức: 10 x 2 - 4 - 2 2 - x .
A. 2 x + 14 ( x - 2 ) ( x + 2 )
B. - 2 x + 14 ( x - 2 ) ( x + 2 )
C. 2 x - 14 ( x - 2 ) ( x + 2 )
D. - 2 x - 14 ( x - 2 ) ( x + 2 )
SGK Kết nối tri thức và cuộc sống
22 tháng 7 2023 lúc 9:20
Thực hiện các phép tính cộng, trừ phân thức sau:
a) \(\dfrac{x}{{x + 3}} + \dfrac{{2 - x}}{{x + 3}}\) b) \(\dfrac{{{x^2}y}}{{x - y}} - \dfrac{{x{y^2}}}{{x - y}}\) c) \(\dfrac{{2x}}{{2x - y}} + \dfrac{y}{{y - 2x}}\)
\(a,\dfrac{x}{x+3}+\dfrac{2-x}{x+3}\\ =\dfrac{x+2-x}{x+3}\\ =\dfrac{2}{x+3}\\b,\dfrac{x^2y}{x-y}-\dfrac{xy^2}{x-y}\\ =\dfrac{x^2y-xy^2}{x-y}\\ =\dfrac{xy\left(x-y\right)}{x-y}\\ =xy\\ c,\dfrac{2x}{2x-y}+\dfrac{y}{y-2x}\\=\dfrac{2x}{2x-y}-\dfrac{y}{2x-y}\\ =\dfrac{2x-y}{2x-y}\\ =1 \)
Đúng 1
Bình luận (0)
`a, x/(x+3) + (2-x)/(x+3) = (x+2-x)/(x+3) = 2/(x+3)`
`b, (x^2y)/(x-y) - (xy^2)/(x-y) = (x^2y-xy^2)/(x-y) = (xy(x-y))/(x-y)= xy`
`c, (2x)/(2x-y) - (y)/(2x-y)`
`= (2x-y)/(2x-y) = 1`
Đúng 0
Bình luận (0)