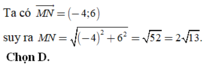Tìm khoảng cách giữa hai điểm trên mặt phẳng tọa độ, biết: P( x 1 ; y 1 ), Q( x 2 ; y 2 )

Những câu hỏi liên quan
Tìm khoảng cách giữa hai điểm trên mặt phẳng tọa độ, biết: A(1; 1), B(5; 4)
Ta có: A B 2 = A C 2 + B C 2 = 5 - 1 2 + 4 - 1 2 = 16 + 9 = 25
AB = 25 = 5
Đúng 0
Bình luận (0)
Tìm khoảng cách giữa hai điểm trên mặt phẳng tọa độ, biết: M(-2; 2), N(3; 5)
Ta có: M N 2 = M D 2 + N D 2 = 3 + 2 2 + 3 - 2 2 = 25 + 9 = 34
AB = 34 ≈ 5,83
Đúng 0
Bình luận (0)
Trên mặt phẳng tọa độ Oxy, vẽ đồ thị (d) của hàm số y=-x+2
Tìm tọa độ của những điểm nàm trên đường thẳng (d) sao cho khoảng cách từ điểm đó đến trục Ox bằng hai lần khoảng cách từ điểm đó đến trục Oy
Cho điểm M(1 ; 4 ; 2) và mặt phẳng (α): x + y + z -1 = 0.
a) Tìm tọa độ điểm H là hình chiếu vuông góc của điểm M trên mặt phẳng (α) ;
b) Tìm tọa độ điểm M' đối xứng với M qua mặt phẳng (α).
c) Tính khoảng cách từ điểm M đến mặt phẳng (α).
a) Xét đường thẳng d qua M và d ⊥ (α).
Khi đó H chính là giao điểm của d và (α).
Vectơ (1 ; 1 ; 1) là vectơ pháp tuyến của (α) nên
là vectơ chỉ phương của d.
Phương trình tham số của đường thẳng d có dạng: .
Thay tọa độ x ; y ; z của phương trình trên vào phương trình xác định (α), ta có:
3t + 6 = 0 => t = -2 => H(-1 ; 2 ; 0).
b) Gọi M'(x ; y ; z) là điểm đối xứng của M qua mặt phẳng (α), thì hình chiếu vuông góc H của M xuống (α) chính là trung điểm của MM'.
Ta có:
=> x = -3 ;
=> y = 0 ;
=> z = -2.
Vậy M'(-3 ; 0 ;2).
c) Tính khoảng cách từ điểm M đến mặt phẳng (α) bằng 2 cách sau:
Cách 1: Áp dụng công thức ta có:
.
Cách 2: Khoảng cách từ M đến (α) chính là khoảng cách MH:
d(M,(α) )= MH = .
Đúng 0
Bình luận (0)
Cho điểm M(1 ; 4 ; 2) và mặt phẳng (α): x + y + z -1 = 0.
a) Tìm tọa độ điểm H là hình chiếu vuông góc của điểm M trên mặt phẳng (α) ;
b) Tìm tọa độ điểm M' đối xứng với M qua mặt phẳng (α).
c) Tính khoảng cách từ điểm M đến mặt phẳng (α).
a) Xét đường thẳng d qua M và d ⊥ (α).
Khi đó H chính là giao điểm của d và (α).
Vectơ (1 ; 1 ; 1) là vectơ pháp tuyến của (α) nên
là vectơ chỉ phương của d.
Phương trình tham số của đường thẳng d có dạng: .
Thay tọa độ x ; y ; z của phương trình trên vào phương trình xác định (α), ta có:
3t + 6 = 0 => t = -2 => H(-1 ; 2 ; 0).
b) Gọi M'(x ; y ; z) là điểm đối xứng của M qua mặt phẳng (α), thì hình chiếu vuông góc H của M xuống (α) chính là trung điểm của MM'.
Ta có:
=> x = -3 ;
=> y = 0 ;
=> z = -2.
Vậy M'(-3 ; 0 ;2).
c) Tính khoảng cách từ điểm M đến mặt phẳng (α) bằng 2 cách sau:
Cách 1: Áp dụng công thức ta có:
.
Cách 2: Khoảng cách từ M đến (α) chính là khoảng cách MH:
d(M,(α) )= MH = .
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, tính khoảng cách giữa hai điểm M (1;-2) và N (- 3; 4)
A. MN = 4
B. MN=6
C. M N = 3 6 .
D. M N = 2 13 .
Trong mặt phẳng tọa độ Oxy, tính khoảng cách giữa hai điểm M( 1; -2) và N ( -3; 4)
A. MN= 4
B. MN = 6
C. M N = 3 6 .
D. M N = 2 13 .
Ta có M N → = − 4 ; 6 suy ra M N = − 4 2 + 6 2 = 52 = 2 13 .
Chọn D
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ; cho 2 điểm A(1; 2) và B(4; 6). Tính khoảng cách giữa hai điểm đó.
A. 4
B. 2
C. 3
D. 5
Cho hai hàm số sau y = x + 1 và y = – 2x + 4 a/ Vẽ trên cùng một mặt phẳng tọa độ đồ thị hai hàm số trên. b/ Tìm tọa độ giao điểm của hai hàm số đó. c/ Tính khoảng cách từ gốc tọa độ đến đường thẳng y = – 2x + 4 (kết quả làm tròn đến chữ số thập phân thứ 3) ( giúp mình với :((( )
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x+1=-2x+4\\y=x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
Đúng 1
Bình luận (1)