Một hình lăng trụ đứng có đáv là đa giác n cạnh. Hãy tính:
a) Số đỉnh của hình lăng trụ;
b) Số cạnh của hình lăng trụ;
c) Số mặt của hình lăng trụ
một hình lăng trụ đứng có đáy là đa giác n cạnh , hãy tính
a, số đỉnh của lăng trụ
b, số cạnh của lăng trụ
c, số mặt của lăng trụ
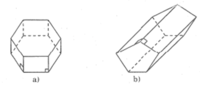
Quan sát các hình lăng trụ đứng trên hình vẽ rồi điền số thích hợp vào các ô trống ở bảng sau:
| Hình lăng trụ | Số cạnh của một đáy (n) | Số mặt (m) | Số đỉnh (d) | Số cạnh (c) |
| a) | ||||
| b) |
Có thể tìm được một lăng trụ đứng có 15 đỉnh hay không?
| Hình lăng trụ | Số cạnh của một đáy (n) | Số mặt (m) | Số đỉnh (d) | Số cạnh (c) |
| a) | 6 | 8 | 12 | 18 |
| b) | 5 | 7 | 10 | 15 |
Không thể làm một hình lăng trụ đứng có 15 đỉnh vì d = 2n (số đỉnh của hình lăng trụ là một số chẵn)
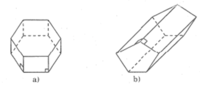
Quan sát các hình lăng trụ đứng trên hình vẽ rồi điền số thích hợp vào các ô trống ở bảng sau:
| Hình lăng trụ | Số cạnh của một đáy (n) | Số mặt (m) | Số đỉnh (d) | Số cạnh (c) |
| a) | ||||
| b) |
Hình lăng trụ đứng có 20 đỉnh thì có bao nhiêu mặt ,bao nhiêu cạnh?
| Hình lăng trụ | Số cạnh của một đáy (n) | Số mặt (m) | Số đỉnh (d) | Số cạnh (c) |
| a) | 6 | 8 | 12 | 18 |
| b) | 5 | 7 | 10 | 15 |
Số cạnh của một đáy là: n = d/2 = 20/2 = 10 cạnh
Hình lăng trụ có 20 đỉnh thì :
Số mặt là m = n + 2 = 10 + 2 = 12 mặt
Số cạnh là c = 3n = 3.10 = 30 cạnh
Một hình lăng trụ đứng ABC.A'B'C'(đáy là tam giác đều ABC) ở bên trong một hình trụ. Các đỉnh A, B, C, A', B', C' thuộc hình trụ. Hình lăng trụ đứng và hình trụ có cùng chiều cao. Cho biết chu vi tam giác ABC là 6cm, thể tích của hình lăng trụ đứng là 123 cm³. Hãy tính chiều cao và thể tích của hình trụ( kết quả làm tròn đến hàng đơn vị)
Chú ý: Thể tích hình trụ đứng = diện tích đáy nhân với chiều cao.
Diện tích tam giác đều là: AB^2√3/4
Thể tích hình trụ = diện tích đáy nhân với chiều cao.
AB=2cm
=>S ABC=căn 3(cm2)
=>h=12(cm)
Cho một hình lăng trụ đứng có đáy là tam giác đều. Thể tích của hình lăng trụ là V. Để diện tích toàn phần của hình lăng trụ nhỏ nhất thì cạnh đáy của lăng trụ là bao nhiêu?
A. 6 V 3
B. 2 V 3
C. 4 V 3
D. V 3
Đáp án C
Phương pháp:
Thể tích hình lăng trụ V = Sh
Diện tích toàn phần của lăng trụ: Stp = Sxq + 2.Sđáy
Cách giải:
Giả sử hình lăng trụ có đáy là tam giác đều cạnh a, có chiều cao h.


Dấu “=” xảy ra khi và chỉ khi
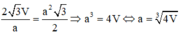
Một hình lăng trụ đứng có đáy là một tam giác vuông. Độ dài hai cạnh góc vuông của đáy là 3cm và 4cm. Chiều cao của lăng trụ là 8cm. Hãy tính diện tích xung quanh, diện tích toàn phần và thể tích của hình lăng trụ đó.
Áp dụng định lí Py - Ta - Go , độ dài cạnh còn lại của mặt đáy tam giác là :
\(\sqrt{3^2+4^2}=5\left(cm\right)\)
Diện tích xung quanh hình lăng trụ đứng :
\(S_{xq}=\left(3+4+5\right).8=96\left(cm^2\right)\)
Diện tích toàn phần :
\(S_{tp}=96+\left(3.4\right)=108\left(cm^2\right)\)
Thể tích :
\(V=\dfrac{3.4}{2}.8=48\left(cm^3\right)\)
a) Cho một hình lăng trụ đứng có độ dài cạnh bên là 10 cm và đáy là tam giác. Biết tam giác đó có độ dài các cạnh lần lượt là 4 cm, 5 cm, 6 cm. Tính diện tích xung quanh của hình lăng trụ đứng đã cho.
b) Cho một hình lăng trụ đứng có độ dài cạnh bên là 20 cm và đáy là một hình thang cân. Biết hình thang cân đó có độ dài cạnh bên là 13 cm, độ dài hai đáy lần lượt là 8 cm, 18 cm và chiều cao là 12 cm. Tính diện tích toàn phần (tức là tổng diện tích các mặt) của hình lăng trụ đứng đã cho.
a)

Chu vi đáy hình lăng trụ đứng đó là:
4+5+6=15 (cm)
Diện tích xung quanh hình lăng trụ đứng đó là:
Sxq = 15.10 = 150 (cm2 )
b)
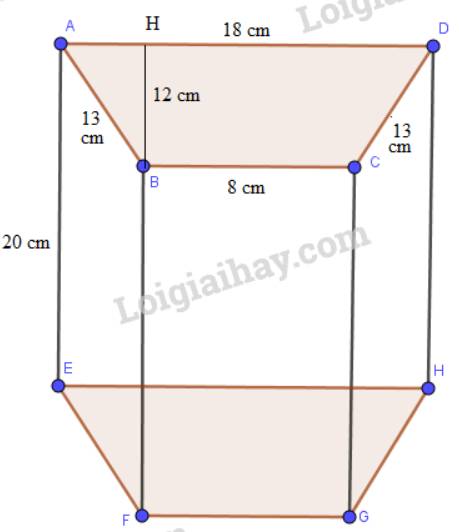
Chu vi đáy là: 8+18+13+13 = 52 (cm)
Diện tích đáy là: Sđáy = (8+18).12:2 = 156 (cm2)
Diện tích toàn phần của lăng trụ đó là:
Stp = Sxq + 2. Sđáy = 52. 20 +2. 156 = 1352 (cm2)
a, một lăng trụ đứng có đáy là một tam giác vuông, các cạnh hóc vuông của tam giác vuông là 3cm, 4cm. chiều cao của hình lăng trụ là 9cm.tính thể tích và diện tích xung quanh, diện tích toàn phần của lăng trụ
b, một lăng trụ đứng có đáy là hình chữ nhật có các kích thước là 3cm, 4cm. chiều cao của lăng trụ là 5cm. tính diện tích xung quanh của lăng trụ
a. Thể tích là:
\(\frac{3x4}{2}\)x 9 = 54 cm3
Trong tam giác vuông ABC (vuông tại A), theo định lý Pytago, ta có cạnh huyền bằng:
\(\sqrt{3^2+4^2}\) = 5 cm
Diện tích xung quanh là:
(3 + 4 + 5) x 9 = 108 cm2
Diện tích toàn phần là:
108 + 3 x 4 = 120 cm2
b. Diện tích xung quanh là:
(3 + 4) x 2 x 5 = 70 cm2
Đáp số : 70 cm2
a. Thể tích là:
\(\dfrac{3x4}{2}\times9=54cm^3\)
Trong tam giác vuông ABC (vuông tại A), theo định lý Pytago, ta có cạnh huyền bằng:
\(\sqrt{3^2+4^2}5cm\)
Diện tích xung quanh là:
(3 + 4 + 5) x 9 = 108 cm2
Diện tích toàn phần là:
108 + 3 x 4 = 120 cm2
b. Diện tích xung quanh là:
(3 + 4) x 2 x 5 = 70 cm2
Đáp số : 70 cm2
Quan sát hình lăng trụ đứng tứ giác ở Hình 9, đọc tên các mặt, các cạnh, các đỉnh và các đường chéo của hình lăng trụ đứng tứ giác đó.
Hình lăng trụ đứng tứ giác ABCD. A’B’C’D’ có:
+) 6 mặt gồm: ABCD; A’B’C’D’; ABB’A’; ADD’A’; BCC’B’; CDD’C’.
+) 12 cạnh gồm: AB; BC;CD;DA;A’B’;B’C’;C’D’; D’A’; AA’; BB’; CC’ ; DD’.
+) 8 đỉnh gồm: A;B;C;D;A’;B’;C’;D’.