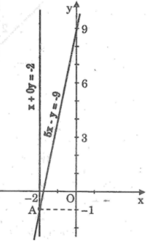
Hệ phương trình x + y = 9 x 2 + y 2 = 41 có:
A. đúng một nghiệm ( 4 ; 5 )
B. đúng một nghiệm 5 ; 4
C. đúng hai nghiệm ( 4 ; 5 ) và 5 ; 4
D. nhiều hơn hai nghiệm
Cho hệ phương trình 2 x - 3 y = 1 4 x + y = 9 . Nghiệm của hệ phương trình là (x, y), tính x - y
A. x - y = -1
B. x - y = 1
C. x - y = 0
D. x - y = 2
Cho hệ phương trình 2 x − 3 y = 1 4 x + y = 9 . Nghiệm của hệ phương trình là (x; y), tính x – y
A. x – y = −1
B. x – y = 1
C. x – y = 0
D. x – y = 2
Ta có:
2 x − 3 y = 1 4 x + y = 9 ⇔ 2 x − 3 y = 1 12 x + 3 y = 27 ⇔ 2 x − 3 y = 1 2 x − 3 y + 12 x + 3 y = 1 + 27 ⇔ 2 x − 3 y = 1 14 x = 28 ⇔ x = 2 y = 1
Vậy hệ đã cho có nghiệm duy nhất (x; y) = (2; 1)
x – y = 2 – 1 = 1
Đáp án: B
Cho hệ phương trình 2 x - 3 y = 1 4 x + y = 9 . Nghiệm của hệ phương trình là (x, y), tính x - y
A. x - y = -1
B. x - y = 1
C. x - y = 0
D. x - y = 2
Cho hệ phương trình:\(\left\{{}\begin{matrix}mx+2y=18\\x-y=-6\end{matrix}\right.\) (m là tham số)
a.Giải hệ phương trình trên với m=1
b.Tìm m để hệ phương trình có nghiệm duy nhất (x;y) thỏa mãn 2x+y=9
a. Với `m=1`, ta có HPT: \(\left\{{}\begin{matrix}x+2y=18\\x-y=-6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-y=-6\\3y=24\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=8\end{matrix}\right.\)
b. Theo đề bài `=>` \(\left\{{}\begin{matrix}mx+2y=18\\x-y=-6\\2x+y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}mx+2y=18\\x=1\\y=7\end{matrix}\right.\)
`=> m=4`
a) Thay m=1 vào hệ phương trình, ta được:
\(\left\{{}\begin{matrix}x+2y=18\\x-y=-6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3y=24\\x-y=-6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=8\\x=-6+y=-6+8=2\end{matrix}\right.\)
Cho hệ phương trình \(\left\{{}\begin{matrix}3x+y=2m+9\\x+y=5\end{matrix}\right.\)với m là tham số
a.Giải hệ phương trình khi m=-1
b.Tìm các giá trị nguyên của m để hệ phương trình có nghiệm (x;y) thỏa mãn \(x^2+2y^2=18\)
a) Thay m=-1 vào hệ phương trình, ta được:
\(\left\{{}\begin{matrix}3x+y=7\\x+y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=2\\x+y=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=4\end{matrix}\right.\)
Vậy: Khi m=-1 thì (x,y)=(1;4)
b) Ta có: \(\left\{{}\begin{matrix}3x+y=2m+9\\x+y=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x+y=2m+9\\x=5-y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3\left(5-y\right)+y=2m+9\\x=5-y\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}15-3y+y=2m+9\\x=5-y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2y=2m-6\\x=5-y\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=-m+3\\x=5-\left(-m+3\right)=5+m-3=m+2\end{matrix}\right.\)
Ta có: \(x^2+2y^2=18\)
\(\Leftrightarrow\left(m+2\right)^2+2\cdot\left(-m+3\right)^2=18\)
\(\Leftrightarrow m^2+4m+4+2\left(m^2-6m+9\right)-18=0\)
\(\Leftrightarrow m^2+4m-14+2m^2-12m+18=0\)
\(\Leftrightarrow3m^2-8m+4=0\)
\(\Leftrightarrow3m^2-2m-6m+4=0\)
\(\Leftrightarrow m\left(3m-2\right)-2\left(3m-2\right)=0\)
\(\Leftrightarrow\left(3m-2\right)\left(m-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}3m-2=0\\m-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3m=2\\m=2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{2}{3}\\m=2\end{matrix}\right.\)
Cho hệ Phương trình mx+4y=9 và x+my=8
Với giá trị nào của m để hệ Phương trình có nghiệm (x,y) Thỏa mãn hệ thức 2x+y+38/m2-4=3
Cho hệ phương trình x + 0 y = - 2 5 x - y = - 9
Nghiệm của hệ phương trình này có phải là nghiệm của phương trình 3x – 7y = 1 hay không?
Thay x = -2, y = -1 vào phương trình 3x – 7y = 1, ta có:
3.(-2) – 7.(-1) = -6 + 7 = 1
Vậy x và y thỏa phương trình 3x – 7y = 1 nên (x; y) = (-2; -1) là nghiệm của phương trình 3x – 7y = 1.
Giải hệ phương trình sau:
{15/x - 7/y = 9
{4/x + 9/y = 35
\(\left\{{}\begin{matrix}\dfrac{15}{x}-\dfrac{7}{y}=9\\\dfrac{4}{x}+\dfrac{9}{y}=35\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{60}{x}-\dfrac{28}{y}=36\\\dfrac{60}{x}+\dfrac{135}{y}=525\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{-163}{y}=-489\\\dfrac{4}{x}+\dfrac{9}{y}=35\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{1}{3}\\x=\dfrac{1}{2}\end{matrix}\right.\)
Giải hệ phương trình x-y=-9 và x+y=11
\(\left\{{}\begin{matrix}x-y=-9\\x+y=11\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2x=2\\x+y=11\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=11-x=10\end{matrix}\right.\)
Giải hệ phương trình:
\(\left\{{}\begin{matrix}x-y=-9\\x+y=11\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-9+y\\-9+y+y=11\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-9+y\\2y-9=11\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-9+y\\2y=20\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-9+10\\y=10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=10\end{matrix}\right.\)
Cho hệ phương trình x + 0 y = - 2 5 x - y = - 9
Minh họa hình học tập nghiệm của hệ phương trình đã cho. Từ đó xác định nghiệm của hệ.
Ta có:
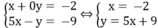
*Vẽ đường thẳng x = -2 song song với trục tung
*Vẽ đường thẳng y = 5x + 9
Cho x = 0 thì y = 9 ⇒ (0; 9)
Cho y = 0 thì x = - 9/5 = -1,8
Hai đường thẳng y = 5x + 9 và x = -2 cắt nhau tại A(-2; -1). Vậy hệ phương trình có một nghiệm duy nhất (x; y) = (-2; -1).