Cho hàm số y = x4 – 2x2 + 3. Tìm các khoảng đồng biến của hàm số
A. (-∞; -1) và (0; 1)
B. (-1; 0) và (1; +∞)
C. (-∞; 0) và (1; +∞)
D. R
Hàm số y = x4 – 2x2 + 3 đồng biến trên các khoảng nào?
A. R
B. (-1 ; 0) và (0 ; 1).
C. (-∞; -1) và (0 ; 1).
D. (-1 ;0) và (1; +∞)
Đáp án D.
y = x4 – 2x2 + 3 => y’ = 4x3 – 4x.
y’ = 0 <=> 4x3 – 4x = 0 <=>![]()
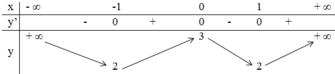
Vậy hàm số đồng biến trên khoảng (-1 ;0) và (1; +∞).
Hàm số y = x 4 − 2 x 2 + 2 đồng biến trên các khoảng
A. − ∞ ; − 1 và (-1;0)
B. )-1;0) và (0;1)
C. − ∞ ; 0 và (0;1)
D. (-1;0) và 1 ; + ∞
Đáp án D
Ta có: y ' = 4 x 3 − 4 x = 4 x x 2 − 1 > 0 ⇔ x ∈ − 1 ; 0 ∪ 1 ; + ∞ ⇒ Hàm số đồng biến trên các khoảng − 1 ; 0 và 1 ; + ∞
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 4 − 2 x 2 + 2 m 2 − 1 x + 5 đồng biến trên khoảng 1 ; + ∞ .
A. − 2 2 ≤ m ≤ 2 2
B. − 2 2 < m < 2 2
C. m < − 2 2 hoặc m > 2 2
D. m ≤ − 2 2 hoặc m ≥ 2 2
Đáp án D
Hàm số đồng biến trên khoảng:
1 ; + ∞ ⇔ y ' ≥ 0 , ∀ x ∈ 1 ; + ∞ .
Ta có: y ' = 4 x 3 − 4 x + 2 m 2 − 1 ⇒ y ' ≥ 0
⇔ f x = 4 x 3 − 4 x − 1 ≥ − 2 m 2 , x ∈ 1 ; + ∞ ⇒ − 2 m 2 ≤ min 1 ; + ∞ f x .
Ta có: f ' x = 12 x 2 − 4 ⇒ f ' x = 0 ⇔ x = ± 1 3 .
Có bảng biến thiên hàm số f(x) như sau:
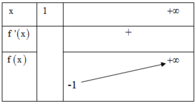
Từ bảng biến thiên , suy ra f x > − 1 , x ∈ 1 ; + ∞
⇒ − 2 m 2 ≤ − 1 ⇔ m 2 ≥ 1 2 ⇔ m ≥ 2 2 m ≤ − 2 2
Cho hàm số y = -x4 + 2x2. Hỏi hàm số đã cho đồng biến trên khoảng nào sau đây?
A. (-∞; +∞)
B. (3; +∞)
C. (-∞; -1)
D. (0; 2)
Đáp án C.
Hàm số y = -x4 + 2x2 có y’ = -4x3 + 4x, y’ ≥ 0
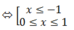
Vậy hàm số đã cho đồng biến trên (-∞; -1)
Hàm số y = x 4 - 2 x 2 đồng biến trên khoảng nào trong các khoảng sau
![]()
![]()
![]()
![]()
Cho hàm số y = x 4 - 2 x 2 + 1 . Xét các mệnh đề sau đây
1) Hàm số có 3 điểm cực trị;
2) Hàm số đồng biến trên các khoảng - 1 ; 0 ; 1 ; + ∞
3) Hàm số có 1 điểm cực trị;
4) Hàm số nghịch biến trên các khoảng - ∞ ; - 1 ; 0 ; 1
Có bao nhiêu mệnh đề đúng trong bốn mệnh đề trên?
A. 2
B. 1
C. 4
D. 3
cho hàm số y = 2x2 - (m - 1 )x +3, m là tham số
a. tìm khoảng đồng biến, nghịch biến của hàm số
b/ tìm các giái trị của m để hàm số đồng biến trên khoảng 1;+∞
c. tìm m để hàm số nghịch biến trên khoàng -4;8
d. tìm m để giá trị nhỏ nhất của hàm số là 9
Hàm số y = x 4 - 2 x 2 đồng biến trên khoảng
A. (-∞;1).
B. (0;+∞).
C. (0;1) và (1;+∞).
D. (-1;0) và (1;+∞).
Hàm số y = x 4 - 2 x 2 đồng biến trên khoảng
A. ![]() .
.
B. ![]() .
.
C. ![]() và
và ![]() .
.
D. ![]() và
và ![]() .
.