Cho hàm số y = x 3 + 1 . Gọi Δ x là số gia đối số tại x và Δ y là số gia tương ứng của hàm số. Tính Δ y Δ x
A. 3 x 2 − 3 x Δ x + Δ x 3
B. 3 x 2 + 3 x Δ x − Δ x 2
C. 3 x 2 + 3 x Δ x + Δ x 3
D. 3 x 2 + 3 x Δ x + Δ x 2
Cho hàm số y = x 3 + 1 . Gọi ∆ x là số gia đối số tại x và ∆ y là số gia tương ứng của hàm số. Tính ∆ y ∆ x
A. 3 x 2 - 3 x ∆ x + ∆ x 3
B. 3 x 2 + 3 x ∆ x - ∆ x 2
C. 3 x 2 + 3 x ∆ x + ∆ x 3
D. 3 x 2 + 3 x ∆ x + ∆ x 3
Đáp án D.
Ta có ∆ y = x + ∆ x 3 + 1 - x 3 + 1 = 3 x 2 . ∆ x + 3 x . ∆ x 2 + ∆ x 3
→ ∆ y ∆ x = ∆ x . 3 x 2 + 3 x ∆ x + ∆ x 2 ∆ x = 3 x 2 + 3 x ∆ x + ∆ x 2
Cho hàm số 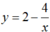 có đồ thị (H). Đường thẳng Δ vuông góc với đường thẳng d: y = -x + 2 và tiếp xúc với (H) thì phương trình của Δ là
có đồ thị (H). Đường thẳng Δ vuông góc với đường thẳng d: y = -x + 2 và tiếp xúc với (H) thì phương trình của Δ là
A. y = x + 4.
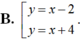
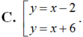
D. Không tồn tại.
Chọn C.
Đạo hàm: 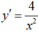
Đường thẳng Δ vuông góc với đường thẳng d: y = -x + 2 nên có hệ số góc bằng 1.
Ta có phương trình 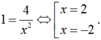
Tại M(2; 0). Phương trình tiếp tuyến là y = x – 2.
Tại N(-2; 4). Phương trình tiếp tuyến là y = x + 6.
Cho hàm số f ( x ) = x 2 + 2 x ,có ∆x là số gia của đối số tại x=1, ∆y là số gia tương ứng của hàm số. Khi đó ∆y bằng:
A. ( ∆ x ) 2 + 2 ∆ x
B. ( ∆ x ) 2 + 4 ∆ x
C. ( ∆ x ) 2 + 2 ∆ x - 3
D. 3
∆y=f(1+∆x)-f(1)=(1+∆x)2+2(1+∆x)-(1+2)=(∆x)2+4∆x
Đáp án B
Chú ý. Tránh các sai lầm thay trực tiếp ∆x hoặc 1 vào hàm (A,D) hoặc lấy hiệu của f(∆x) và f(1) (C)
Cho hàm số y = x 3 + 3 x 2 − 1 có đồ thị (C). Gọi Δ là tiếp tuyến của (C) tại điểm có hoành độ x 0 = 0 , B là giao điểm thứ hai của Δ với (C). Tính diện tích tam giác OAB.
A. 1 4 .
B. 3 2 .
C. 1 2 .
D. 2.
Đáp án B
y ' = 3 x 2 + 6 x ;
Phương trình tiếp tuyến của (C) tại điểm x 0 = 0 là Δ : y = − 1 .
Giao điểm của (C) và Δ là nghiệm của hệ phương trình
y = − 1 y = x 3 + 3 x 2 − 1 ⇔ x 3 + 3 x 2 − 1 = − 1 y = − 1 ⇔ x = 0 x = − 3 y = − 1
Do đó giao điểm B − 3 ; − 1 .
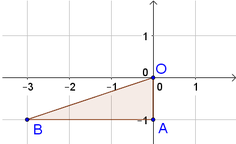
Tam giác OAB vuông tại A nên S O A B = 1 2 . O A . A B = 1 2 .1.3 = 3 2 .
Tiếp tuyến Δ của đồ thị hàm số y = 3 x − 2 x + 2 tại điểm có hoành độ x 0 = − 3 . Khi đó Δ có hệ số góc k là
A. k = 9
B. k = 10
C. k = 11
D. k = 8
Đáp án D
Ta có: y ' = 8 x + 2 2 ⇒ k 0 = y ' − 3 = 8.
Đường thẳng Δ có phương trình y = 2 x + 1 cắt đồ thị của hàm số y = x 3 − x + 3 tại hai điểm A và B với tọa độ được kí hiệu lần lượt là A x A ; y A và B x B ; y B trong đó x B < x A . Tìm x B + y B ?
A. x B + y B = − 5
B. x B + y B = 4
C. x B + y B = − 2
Đáp án A
Hoành độ giao điểm của đường thẳng Δ có phương trình y = 2 x + 1 và đồ thị của hàm số y = x 3 − x + 3 là nghiệm PT:
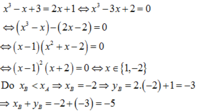
Phương trình tiếp tuyến với đồ thị hàm số y = x + 1 x − 1 song song với đường thẳng Δ : 2 x + y + 1 = 0 là
A. 2 x + y = 0
B. 2 x + y + 7 = 0
C. 2 x + y − 7 = 0
D. − 2 x − y − 1 = 0
Đáp án là C
y ' = − 2 x − 1 2 . Gọi M x 0 ; y 0 ∈ C là tiếp điểm.
Vì tiếp tuyến song song với đường thẳng y = − 2 x − 1 nên:
− 2 x 0 − 1 2 = − 2 ⇔ x 0 − 1 2 = 1 ⇔ x 0 = 2 ⇒ y 0 = 3 x 0 = 0 ⇒ y 0 = − 1
Phương trình tiếp tuyến cần tìm: 2 x + y − 7 = 0.
Đồ thị hàm số y = f ( x ) = a x 2 + b x + c được cho trong hình 47. Kí hiệu Δ = b 2 - 4 a c là biệt số của f(x). Trong các khẳng định sau, khẳng định nào sai?
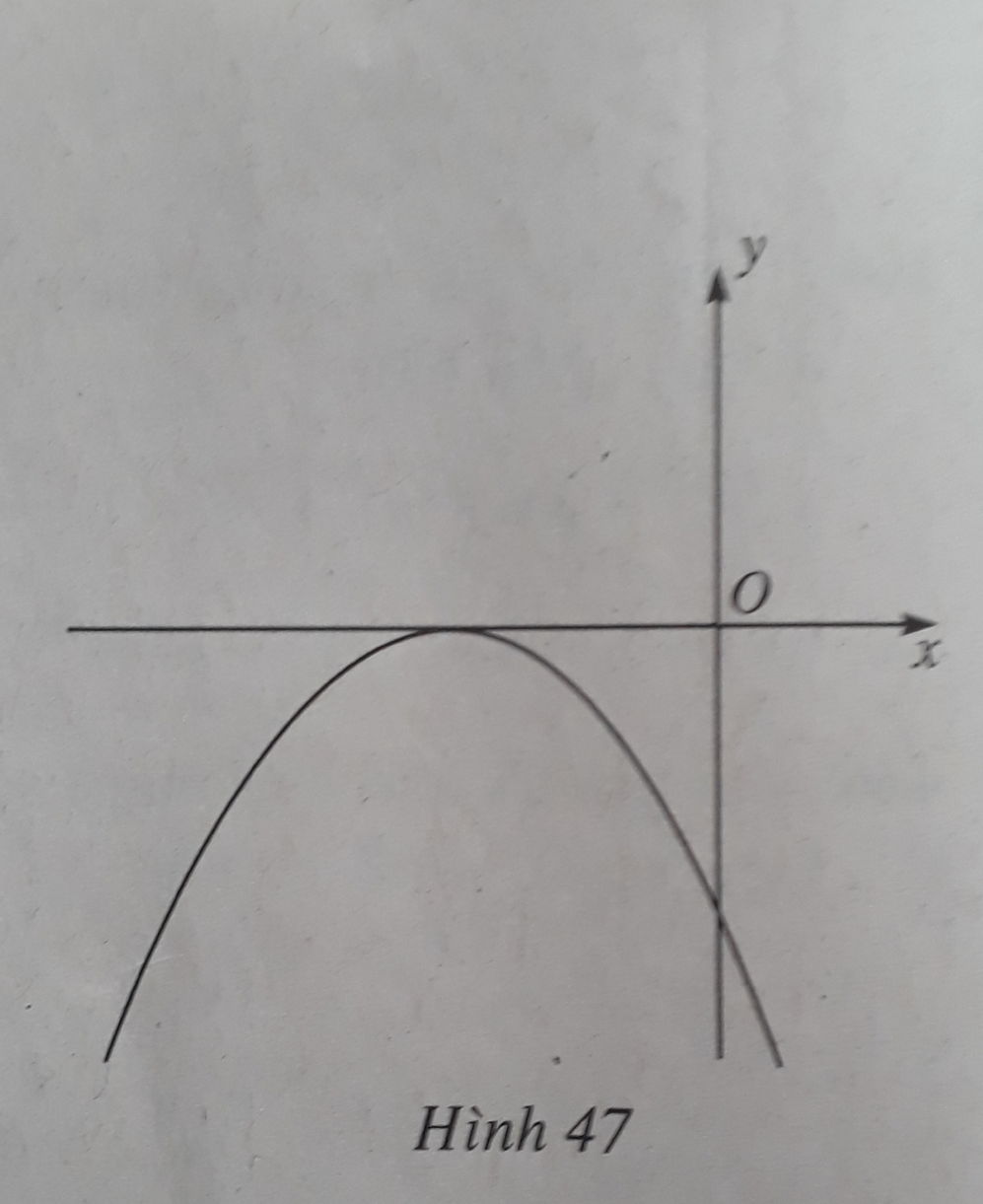
A. a, b trái dấu
B. f(x) ≤ 0, ∀x
C. a < 0, c < 0
D. Δ = 0, a < 0
số gia của hàm số y = f(x) = \(\dfrac{^{x^3}}{2}\) ứng với số gia △t của đối số tại x\(_0\) = -1 là :
Số gia của hàm \(f\left(x\right)\) phải ứng với số gia \(\Delta x\) của đối số chứ sao lại \(\Delta t\), em kiểm tra lại đề bài