Đáp án A
Hoành độ giao điểm của đường thẳng Δ có phương trình y = 2 x + 1 và đồ thị của hàm số y = x 3 − x + 3 là nghiệm PT:
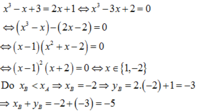
Đáp án A
Hoành độ giao điểm của đường thẳng Δ có phương trình y = 2 x + 1 và đồ thị của hàm số y = x 3 − x + 3 là nghiệm PT:
Đường thẳng d : y = x - 3 cắt đồ thị (C) của hàm số y = x + 1 x - 2 tại hai điểm phân biệt A và B phân biệt. Gọi d 1 , d 2 lần lượt là khoảng cách từ A và B đến đường thẳng D: x-y=0. Tính d = d 1 + d 2
A. d = 3 2
B. d = 3 2 2
C. d = 6
D. d = 2 2
Cho hàm số y=f(x); y=f(f(x)); y = f x 2 + 4 có đồ thị lần lượt là C 1 , C 2 , C 3 . Đường thẳng x=1 cắt C 1 , C 2 , C 3 lần lượt tại M,N,P. Biết phương trình tiếp tuyến của C 1 tại M và của C 2 tại N lần lượt là y=3x+2 vày=12x-5. Biết phương trình tiếp tuyến của C 3 tại P có dạng y=ax+b Tìm a+b
A. 7.
B. 9.
C. 8.
D. 6.
Cho hàm số y = x + 2 2 x + 3 có đồ thị (C). Đường thẳng (d) có phương trình y = a x + b là tiếp tuyến của (C), biết (d) cắt trục hoành tại A và cắt trục tung tại B sao cho tam giác OAB cân tại O, với O là gốc tọa độ. Tính a+ b
A. 0
B. -2
C. -1
D. -3
Cho hàm số y = x + 2 2 x + 3 có đồ thị (C). Đường thẳng d có phương trình y = a x + b là tiếp tuyến của (C), biết d cắt trục hoành tại A và cắt trục tung tại B sao cho tam giác OAB cân tại O, với O là gốc tọa độ. Tính a+b
A. -1
B. -2
C. 0
D. -3
Cho hai hàm số y=f(x) và y=g(x) là hai hàm số liên tục trên ℝ có đồ thị hàm số y=f’(x) là đường cong nét đậm, đồ thị hàm số y=g’(x) là đường cong nét mảnh như hình vẽ. Gọi ba giao điểm A, B, C của y=f’(x) và y=g’(x) trên hình vẽ lần lượt có hoành độ là a, b, c. Tìm giá trị nhỏ nhất của hàm số h(x)=f(x)-g(x) trên đoạn [a;c]

A. m i n h x a ; c = h 0
B. m i n h x a ; c = h a
C. m i n h x a ; c = h b
D. m i n h x a ; c = h c
Đường thẳng d: y=x+a luôn cắt đồ thị hàm số y = - x + 1 2 x - 1 H tại hai điểm phân biệt A, B. Gọi k 1 ; k 2 lần lượt là hệ số góc của các tiếp tuyến với (H) tại A và B. Tìm a để tổng k 1 + k 2 đạt giá trị lớn nhất.
A. a = 1
B. a = 2
C. a = -5
D. a = -1
Cho 3 hàm số y = f x , y = f f x , y = f x 2 + 4 có đồ thị lần lượt là C 1 , C 2 , C 3 . Đường thẳng x = 1 cắt C 1 , C 2 , C 3 lần lượt tại các điểm M, N, P. Biết rằng phương trình tiếp tuyến của C 1 tại M, của C 2 tại N và của C 3 tại P lần lượt là y = 3 x + 2 , y = 12 x - 5 v à y = a x + b . Tổng a + b bằng
A. 8
B. 7
C. 9
D. -1
Cho hàm số y=f(x) có đồ thị là (C), hàm số y=f'(x) có đồ thị như hình vẽ bên. Tiếp tuyến với (C) tại điểm có hoành độ x=2 cắt (C) tại hai điểm phân biệt có hoành độ lần lượt là a,b
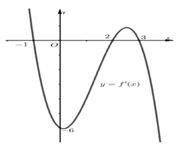
Giá trị ( a - b ) 2 thuộc khoảng nào dưới đây
A. ( 0 ; 9 )
B. ( 12 ; 16 )
C. ( 16 ; + ∞ )
D. ( 9 ; 12 )
Đường thẳng d: y=x+m cắt đồ thị hàm số y = x - 1 x + 1 tại hai điểm phân biệt A, B sao cho O A 2 + O B 2 = 2 , O là gốc tọa độ. Khi đó m thuộc khoảng
A. - ∞ ; 2 - 2 2
B. 0 ; 2 + 2 2
C. 2 + 2 ; 2 + 2 2
D. 2 + 2 2 ; + ∞