Cho ba điểm A, B và C như hình vẽ. Có thể vẽ được bao nhiêu hình bình hành có ba đỉnh là A, B và C?
|
| A. 1 | B. 0 | C. 3 | D. 2 |
Hộp giấy có các mặt là hình vuông ở Hình 1a được vẽ lại với các đỉnh là \(A,B,C,D,A',B',C',D'\) như Hình 1b. Gọi tên cặp mặt phẳng:
a) Có ba điểm chung không thẳng hàng.
b) Là hai mặt phẳng phân biệt và có một điểm chung.
c) Không có bất kì điểm chung nào.
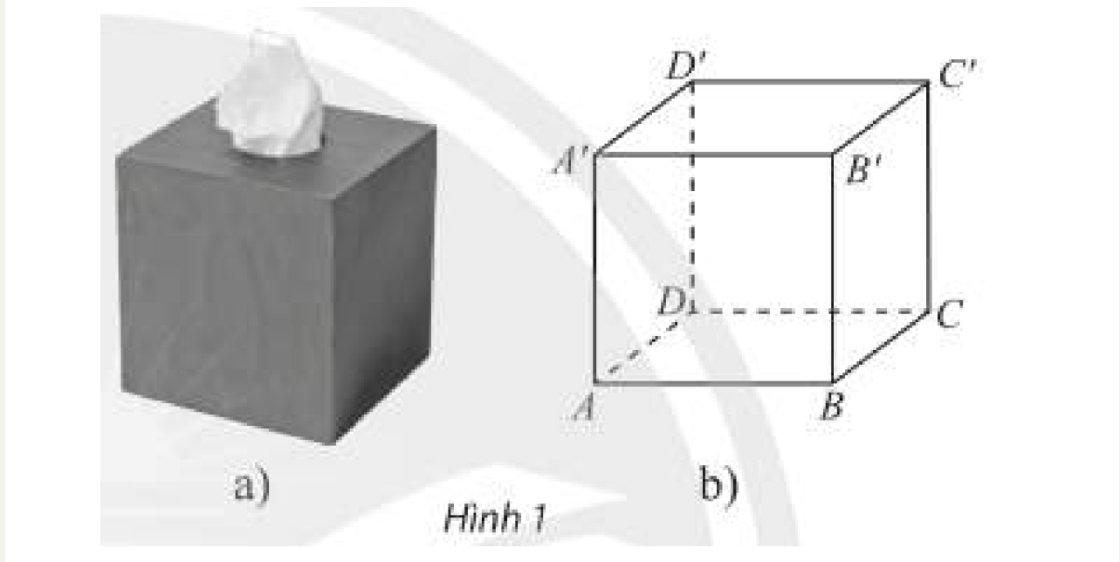
a: (ABC) và (ABD); (A'B'C') và (A'B'D'); (AA'B) và (AA'B'),...
b: Không có hai mp phân biệt nào có 1 điểm chung
c: (ABCD) và (A'B'C'D')
(ABB'A') và (CDD'C')
Cho ba điểm A, B, C trên giấy kẻ ô vuông ở hình bên. Hãy vẽ điểm thứ tư M sao cho A, B,C, M là 4 đỉnh của một hình bình hành.

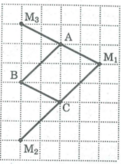
- Nếu hình bình hành nhận AC làm đường chéo vì AB là đường chéo hình vuông có 2 ô vuông nên C M 1 là đường chéo hình vuông cạnh 2 ô vuông và A, M 1 nằm trên một nửa mặt phẳng bờ BC ta có hình bình hành ABC M 1
- Nếu hình bình hành nhận BC làm đường chéo, điểm A cách điểm C ba ô vuông, điểm B cách điểm M 2 là ba ô vuông và trên một nửa mặt phẳng bờ AB ta có hình bình hành AB M 2 C
- Nếu hình bình hành nhận AB làm đường chéo thì điểm M 3 cách điểm B ba ô vuông, M 3 và A nằm trên cùng một nửa mặt phẳng bờ BC ta có hình bình hành ACB M 3
Hình vẽ dưới đây có bao nhiêu bộ ba điểm không thẳng hàng:
A. 1
B. 2
C. 3
D. 4
Hình vẽ dưới đây có bao nhiêu bộ ba điểm không thẳng hàng:
A. 1
B. 2
C. 3
D. 4
@Nae
Bài 01. Vẽ đường tròn (O) rồi lấy bốn điểm A, B, C, D phân biệt trên đường tròn đó. Vẽ các dây cung có hai đầu là hai trong bốn điểm đã cho. Hỏi trong hình vẽ có:
a) Bao nhiêu dây cung?
b) Bao nhiêu cung tròn?
c) Bao nhiêu tam giác có các đỉnh là ba trong bốn điểm trên?
mk cố nghĩ nhưng mk chịu rồi,mk kém hình lắm.
a) có 2 dây cung
b) có 8 cung tròn
c) có 4 tam giác
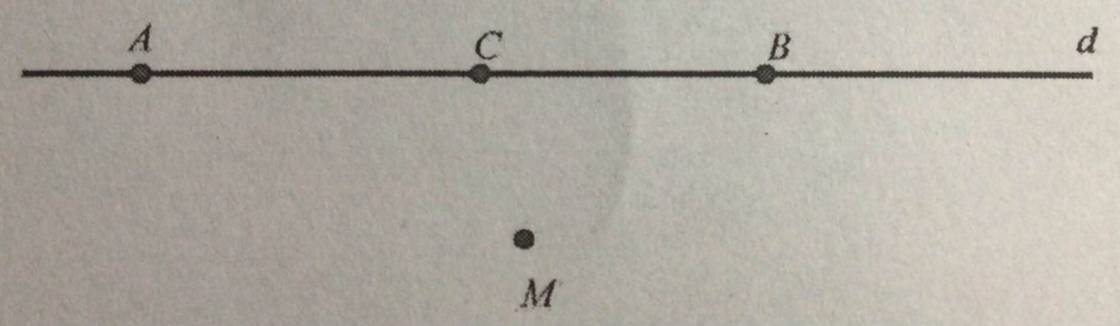
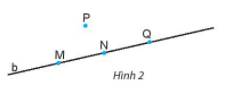
Trên Hình 2, hãy chỉ ra ba điểm thẳng hàng và ba điểm không thẳng hàng.
Dùng thước thẳng để kiểm tra xem ba điểm nào trên Hình 3 là thẳng hàng.
- Vẽ vào vở hai điểm A, B như Hình 4. Em vẽ thêm hai điểm C và D sao cho ba điểm A, B, C thẳng hàng và ba điểm A, B, D cũng thẳng hàng. Hãy vẽ ba vị trí khác nhau của điểm C.
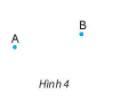
- Trên Hình 2, ba điểm thẳng hàng là: M, N, Q; ba điểm không thẳng hàng là M, N, P
- Trên Hình 3, ba điểm thẳng hàng là M, P, R
- Vẽ hình như sau:
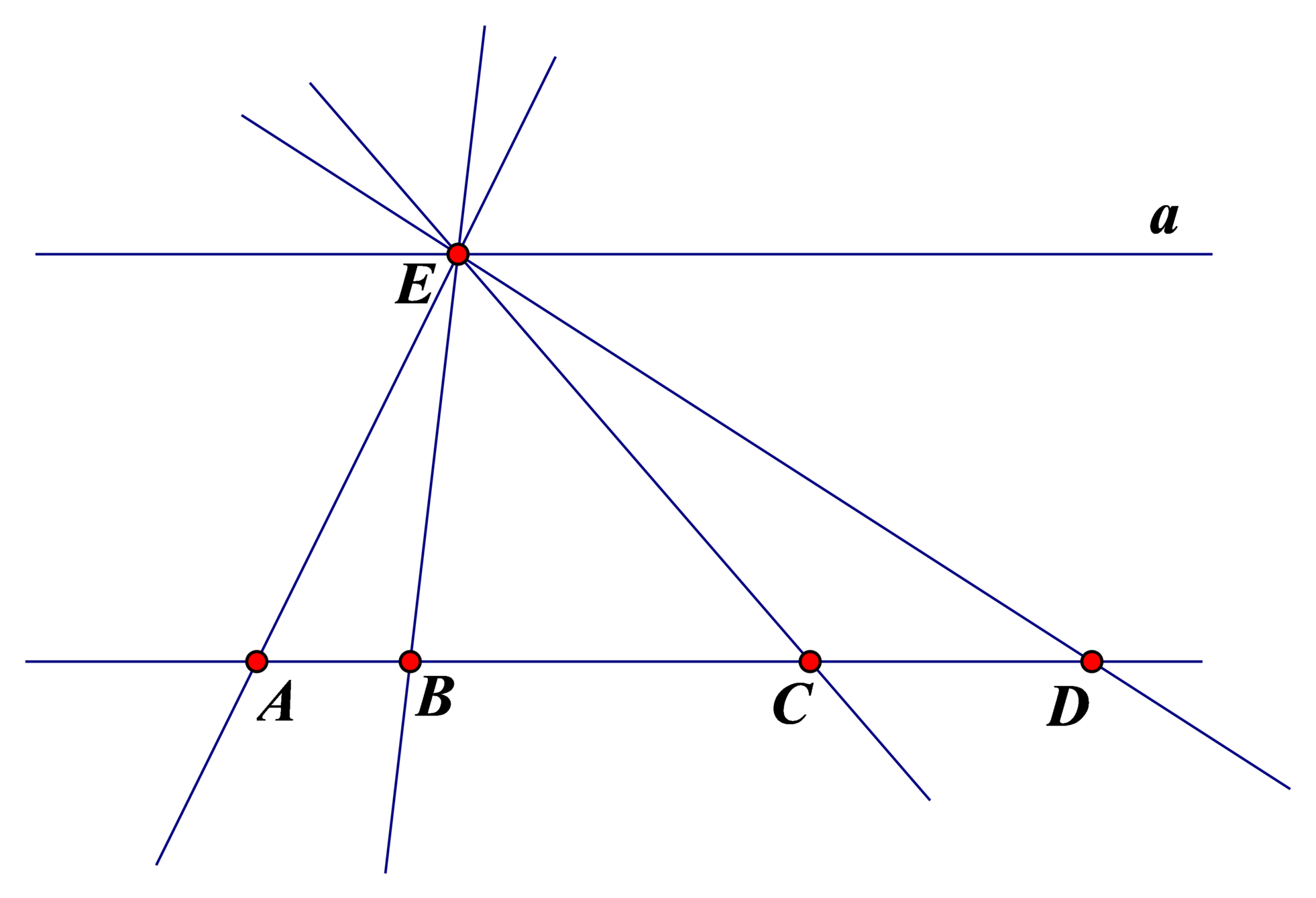
Vẽ hình theo các bước diễn đạt sau:
- Vẽ năm điểm phân biệt A, B, C, D, E sao cho ba điểm A, B, C thẳng hàng; ba điểm B, C, D thẳng hàng; ba điểm B, C, E không thẳng hàng;
- Vẽ các đường thẳng đi qua các cặp điểm. Có bao nhiêu đường thảng phân biệt trong hình vẽ?
- Vẽ đường thẳng a đi qua điểm e và song song với đường thẳng AB. Hỏi đường thẳng a có cắt đường thẳng CD không? Vì sao?
- Có năm đường thảng phân biệt trong hình vẽ, đó là: EA , EB , EC , ED , AB .
- Hai đường thẳng AB và CD trùng nhau; đường thẳng a song song với đường thẳng AB nên cũng song song với đường thẳng CD. Do đó, đường thẳng a không cắt đường thẳng CD.
Cho hình vẽ,biết ba toà nhà A,B,C là ba đỉnh của một tam giác và AC=15cm ,AB=30cm.Người ta lắp đặt tại C một bộ phât sóng Wifi có bán kính hoạt động 50m
a)Hỏi tại B có nhận được tín hiệu Wifi không?
b)Ba tòa nhà A,D,C cũng là ba đỉnh của một tam giác và AD=80m.Hỏi với bộ phát có bán kính như trên tại D có nhận được tín hiệu Wifi không?
Theo đề bài ta có AB > AC
TRong tam giác ABC ta có :
BC < AB + AC
=> BC < 30 + 15 = 45
Nếu đặt tại C máy phát sóng truyền thanh có bán kính hoạt động bằng 50m thì thành phố B nhận được tín hiệu.
b. Ta có Xét tam giác ABC : AD - AC < DC
=> 80 - 15 < DC
=> 65 < DC
Vậy Nếu đặt tại C máy phát sóng truyền thanh có bán kính hoạt động bằng 50m thì thành phố D không nhận được tín hiệu.
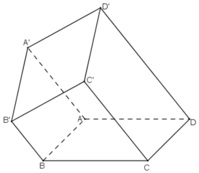
Trong mặt phẳng (α) cho hình bình hành ABCD. Qua A, B, C, D lần lượt vẽ bốn đường thẳng a, b, c, d song song với nhau và không nằm trên (α). Trên a, b và c lần lượt lấy ba điểm A’, B’ và C’ tùy ý.
a) Hãy xác định giao điểm D’ của đường thẳng d với mặt phẳng (A’B’C’).
b) Chứng minh A’B’C’D’ là hình bình hành.
a) Giả sử (A’B’C’) ∩ d = D’
⇒ (A’B’C’) ∩ (C’CD) = C’D’.
+ AA’ // CC’ ⊂ (C’CD)
⇒ AA’ // (C’CD).
AB // CD ⊂ (CC’D)
⇒ AB // (CC’D)
(AA’B’B) có:
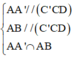 ⇒ (AA’B’B) // (C’CD).
⇒ (AA’B’B) // (C’CD).
Mà (A’B’C’) ∩ (AA’B’B) = A’B’
⇒ (A’B’C’) cắt (C’CD) và giao tuyến song song với A’B’
⇒ C’D’ // A’B’.
b) Chứng minh tương tự phần a ta có B’C’ // A’D’.
Tứ giác A’B’C’D’ có: B’C’ // A’D’ và C’D’ // A’B’
⇒ A’B’C’D’ là hình bình hành.
Cho tam giác ABC vuông tại A ( AC ), đường cao AH. Vẽ hình vuông AHIk (điểm H nằm giữa hai điểm C và I), hai đường thẳng KI và AB cắt nhau tại D
a)Chứng minh rằng AD = AC
b)Vẽ hình bình hành ADEC có hai đường chéo cắt nhau tại O, chứng minh rằng ba điểm O,H,K cùng nằm trên đường trung trực của đoạn AI và tứ giác KOEI là hình thang.
c)Cho AH = 8. Tính AI