Một máy bay đang bay ở độ cao 1700m. Từ một đài quan sát ở mặt đất người ta nhìn thấy máy bay dưới một góc 250 so với mặt đất. Hãy tính khoảng cách từ đài quan sát đến máy bay? (Làm tròn đến mét)

Những câu hỏi liên quan
Hai bạn học sinh A và B đang đứng ở mặt đất bằng phẳng, cách nhau 60m thì nhìn thấy một máy bay trực thăng điều khiển từ xa (ở vị trí C nằm trên tia AB và AC AB). Biết góc “nâng” để nhìn thấy máy bay ở vị trí của B là
50
0
và góc “nâng” để nhìn thấy máy bay ở vị trí của A là
30
0
. Hãy tính độ cao của máy bay lúc đó so với mặt đất? (làm tròn đến chữ số thập phân thứ hai) A. 67,91m B. 69,17m C. 67,19m D....
Đọc tiếp
Hai bạn học sinh A và B đang đứng ở mặt đất bằng phẳng, cách nhau 60m thì nhìn thấy một máy bay trực thăng điều khiển từ xa (ở vị trí C nằm trên tia AB và AC > AB). Biết góc “nâng” để nhìn thấy máy bay ở vị trí của B là 50 0 và góc “nâng” để nhìn thấy máy bay ở vị trí của A là 30 0 . Hãy tính độ cao của máy bay lúc đó so với mặt đất? (làm tròn đến chữ số thập phân thứ hai)
A. 67,91m
B. 69,17m
C. 67,19m
D. 134m

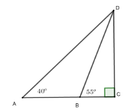
Độ cao của máy bay là CD, độ dài AB = 60m; D A C ^ = 30 0 ; D B C ^ = 50 0
Gọi BC = x => AC = 60 + x
Xét tam giác BDC vuông tại C có:
![]()
Xét tam giác ADC vuông tại C có:
![]()
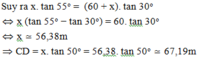
Vậy độ cao của máy bay so với mặt đất là 67,19m
Đáp án cần chọn là: C
Đúng 0
Bình luận (0)
Hai bạn học sinh A và B đang đứng ở mặt đất bằng phẳng, cách nhau 80m thì nhìn thấy một máy bay trực thăng điều khiển từ xa (ở vị trí C nằm trên tia AB và AC AB). Biết góc “nâng” để nhìn thấy máy bay ở vị trí của B là
55
0
và góc “nâng” để nhìn thấy máy bay ở vị trí của A là
40
0
. Hãy tính độ cao của máy bay lúc đó so với mặt đất? (làm tròn đến chữ số thập phân thứ hai) A. 162,75m B. 162,95m C. 163,75m...
Đọc tiếp
Hai bạn học sinh A và B đang đứng ở mặt đất bằng phẳng, cách nhau 80m thì nhìn thấy một máy bay trực thăng điều khiển từ xa (ở vị trí C nằm trên tia AB và AC > AB). Biết góc “nâng” để nhìn thấy máy bay ở vị trí của B là 55 0 và góc “nâng” để nhìn thấy máy bay ở vị trí của A là 40 0 . Hãy tính độ cao của máy bay lúc đó so với mặt đất? (làm tròn đến chữ số thập phân thứ hai)
A. 162,75m
B. 162,95m
C. 163,75m
D. 180m
Độ cao của máy bay là CD, độ dài AB = 80m
Gọi BC = x (x > 0) => AC = 80 + x
Xét tam giác BDC vuông tại C có CD = x . tan 55 0
Xét tam giác ADC vuông tại C có CD = (80 + x). tan 44 0
Suy ra x . tan 55 0 = (80 + x). tan 44 0
=> x ≈ 113,96m
=> CD = 113,96. tan 55 0 ≈ 162,75m
Vậy độ cao của máy bay so với mặt đất là 162,75m
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
Hai bạn An ( vị trí A) và Bình ( vị trí B) đang đứng ở mặt đất bằng phẳng cách nhau 150m thì nhìn thấy một máy bay điều khiển từ xa ( vị trí T). Biết khoảng cách từ An đến máy bay là 80m và khoảng cách từ Bình đến máy bay là 117m. Tính góc nâng để nhìn thấy máy bay tại vị trí của An ( góc TAB) và góc nâng để nhìn thấy may bay từ vị trí của Bình ( góc TBA ). ( kết quả làm tròn đến hàng đơn vị và số đo góc làm tròn đến độ)
Đọc tiếp
Hai bạn An ( vị trí A) và Bình ( vị trí B) đang đứng ở mặt đất bằng phẳng cách nhau 150m thì nhìn thấy một máy bay điều khiển từ xa ( vị trí T). Biết khoảng cách từ An đến máy bay là 80m và khoảng cách từ Bình đến máy bay là 117m. Tính góc nâng để nhìn thấy máy bay tại vị trí của An ( góc TAB) và góc nâng để nhìn thấy may bay từ vị trí của Bình ( góc TBA ). ( kết quả làm tròn đến hàng đơn vị và số đo góc làm tròn đến độ)
Độ cao của máy bay là CD, độ dài AB = 80m
Gọi BC = x (x > 0) => AC = 80 + x
Xét tam giác BDC vuông tại C có CD = x . tan 55 0
Xét tam giác ADC vuông tại C có CD = (80 + x). tan 44 0
Suy ra x . tan 55 0 = (80 + x). tan 44 0
=> x ≈ 113,96m
=> CD = 113,96. tan 55 0 ≈ 162,75m
Vậy độ cao của máy bay so với mặt đất là 162,75m
Nguyễn Văn Phú
Điểm qua sát của một máy bay trực thăng ở giữa hai người quan sát A và B biết khoảng cách giữa hai người này là 400m, góc nâng nhìn thấy máy bay tại vị trí A là 30 độ và tại vị trí B là 40 độ. Tính độ cao của máy bay (kết quả làm tròn đến chữ số thập phân thứ hai) 40 30 B 400m A
Đọc tiếp
Điểm qua sát của một máy bay trực thăng ở giữa hai người quan sát A và B biết khoảng cách giữa hai người này là 400m, góc nâng nhìn thấy máy bay tại vị trí A là 30 độ và tại vị trí B là 40 độ. Tính độ cao của máy bay (kết quả làm tròn đến chữ số thập phân thứ hai)
Gọi C là vị trí của máy bay
Gọi CH là độ cao của máy bay so với mặt đất
=>CH\(\perp\)AB tại H
Ta có hình vẽ sau:
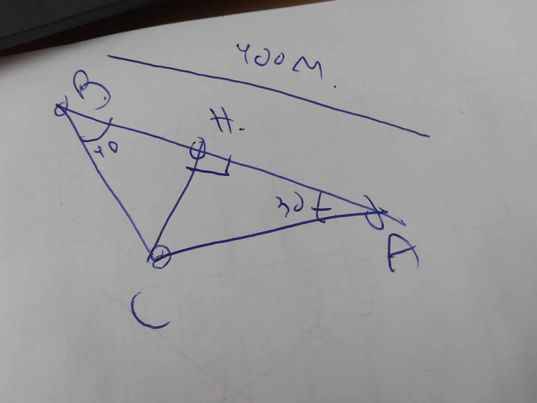
Xét ΔCBA có \(\widehat{CBA}+\widehat{CAB}+\widehat{ACB}=180^0\)
=>\(\widehat{ACB}+30^0+40^0=180^0\)
=>\(\widehat{ACB}=110^0\)
Xét ΔABC có \(\dfrac{BA}{sinACB}=\dfrac{AC}{sinB}=\dfrac{BC}{sinA}\)
=>\(\dfrac{400}{sin110}=\dfrac{AC}{sin40}=\dfrac{BC}{sin30}\)
=>\(AC\simeq273,62\left(m\right);BC\simeq212,84\left(m\right)\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot CA\cdot CB\cdot sinACB\)
\(=\dfrac{1}{2}\cdot273,62\cdot212,84\cdot sin110\simeq27362,57\left(m^2\right)\)
Xét ΔACB có CH là đường cao
nên \(\dfrac{1}{2}\cdot CH\cdot AB=S_{ABC}\)
=>\(CH\cdot\dfrac{400}{2}=27362,57\)
=>\(CH\simeq136,81\left(m\right)\)
Đúng 0
Bình luận (0)
Hai người từ hai vị trí quan sát B và C nhìn thấy một chiếc máy bay trực thăng (ở vị trí A) lần lượt dưới góc 27o ( o ABC 27 ) và 25o ( o ACB 25 )so với phương nằm ngang (trên hình 1). Biết máy bay đang cách mặt đất theo phương thẳng đứng 300 m.
Điểm hạ cánh của 1 máy bay trực thăng ở giữa 2 người quan sát A và B.Biết khoảng cách giữa 2 người này là 400m,góc nâng nhìn thấy máy bay tại vị trí A là 40° và tại vị trí B là 30°.Hãy tìm độ cao của máy bay?(Làm tròn đến mét)
Xem chi tiết
Trên sân bay có một máy bay cất cánh trên đường băng d (từ trái sang phải) và bắt đàu rời mặt đất tại điểm O. Gọi (P) là mặt phẳng vuông góc với mặt đất và cắt mặt đất theo giao tuyến là đường băng d của máy bay. Dọc theo đường băng d cách vị trị máy bay cất cánh O một khoảng 300(m) về phía bên phải có 1 người quan sát A. Biết máy bay chuyển động trong mặt phẳng (P) và độ cao y của máy bay xác định bởi phương trình
y
x
2
(với x là độ...
Đọc tiếp
Trên sân bay có một máy bay cất cánh trên đường băng d (từ trái sang phải) và bắt đàu rời mặt đất tại điểm O. Gọi (P) là mặt phẳng vuông góc với mặt đất và cắt mặt đất theo giao tuyến là đường băng d của máy bay. Dọc theo đường băng d cách vị trị máy bay cất cánh O một khoảng 300(m) về phía bên phải có 1 người quan sát A. Biết máy bay chuyển động trong mặt phẳng (P) và độ cao y của máy bay xác định bởi phương trình y = x 2 (với x là độ dời của máy bay dọc theo đường thẳng d và tính từ O). Khoảng cách ngắn nhất từ người A (đứng cố định) đến máy bay là:
A. 100 3 ( m )
B. 200 (m)
C. 100 5 ( m )
D. 300 (m)
Chọn C.
Phương pháp:
Gắn hệ trục tọa độ, xác định tọa độ điểm M trên parabol y = x 2 để độ dài đoạn AM nhỏ nhất.
Cách giải:
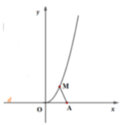
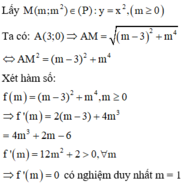
Ta có bảng biến thiên sau:
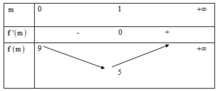
![]()
Đúng 0
Bình luận (0)
Điểm hạ cánh của một máy bay trực thăng ở giữa hai người quan sát A và B. Biết khoảng cách giữa hai người này là 400 m, góc nhìn thấy máy bay tại vị trí A là 40o và tại vị trí B là 32o .Hãy tìm độ cao của máy bay?( làm tròn kết quả đến hàng đơn vị)
Gọi giao điểm của đường nhìn thấy máy bay tại A và B là C.
Vẽ CH vuông góc AB
=>CH là độ cao của máy bay
góc ACB=180-40-32=108 độ
Xét ΔACB có
AB/sin C=AC/sinB=BC/sin A
=>400/sin108=AC/sin32=BC/sin40
=>\(AC\simeq222,9\left(m\right);BC\simeq270,3\left(m\right)\)
\(S_{ABC}=\dfrac{1}{2}\cdot CA\cdot CB\cdot sinC=\dfrac{1}{2}\cdot222.9\cdot270.3\cdot sin108\simeq28650,52\left(m^2\right)\)
Độ cao là:"
28650,52*2/400\(\simeq143\left(m\right)\)
Đúng 1
Bình luận (0)
Một máy bay đang bay ở độ cao so với mặt đất, muốn hạ cánh xuống sân bay. Để đường bay và mặt đất hợp thành một góc an toàn là thì phi công phải bắt đầu hạ cánh từ vị trí cách sân bay bao xa? (làm tròn kết quả đến chữ số phần thập phân)
Đọc tiếp
Một máy bay đang bay ở độ cao so với mặt đất, muốn hạ cánh xuống sân bay. Để đường bay và mặt đất hợp thành một góc an toàn là
thì phi công phải bắt đầu hạ cánh từ vị trí cách sân bay bao xa? (làm tròn kết quả đến chữ số phần thập phân)













