Vì tam giác ABC đồng dạng với tam giác MNP nên;

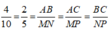
Theo tính chất dãy tỉ số bằng nhau ta có:

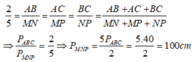
Chọn đáp án C

Chọn A

a) Xét tg AGB có: M là trung điểm của GA (gt); N là trung điểm của GB (gt)

\(\Rightarrow\)MN là đường trung bình của tg \(\Rightarrow\)MN= 1/2 AB \(\Rightarrow\)MN/AB =1/2

CM tương tự: MP/AC =1/2 ; NP/BC =1/2 

Xét tg MNP và tg ABC có: MN/AB =1/2 (cmt); MP/AC =1/2 (cmt); NP/BC =1/2 (cmt)

\(\Rightarrow\)tg MNP \(\infty\)tg ABC (c.c.c) theo tỉ số 1/2

b) tg MNP \(\infty\)tg ABC (c.c.c) theo tỉ số 1/2 \(\Rightarrow\)\(\frac{P\Delta MNP}{P\Delta ABC}=\frac{1}{2}\)mà \(P\Delta MNP=18cm\Rightarrow\)\(P\Delta ABC=\)2.18=36cm

(mk vẽ hình hơi xấu thông cảm nha)

Ai giup vs huhu 

bài1
a) EF=??
b) không đồng dạng
c) không đồng dạng
d) Đồng dạng (vì sao thì bạn nhắn cho mình nha)
các cặp góc bằng nhau ABC=DEF; BCA=EFD; CAB=FDE

bài 2
a) theo tính chất đường trung bình trong mỗi tam giác (không hiểu thì nhắn cho mình)
ta có MN=1/2AB => MN/AB=1/2 (1)
         NM=1/2BC => NP/BC=1/2 (2)
         MP=1/2AC => MP/AC=1/2 (3)

từ (1),(2),(3) => MNP đồng dạng với ABC 
b) vì MNP đồng dạng với ABC với tỉ số k là 2 ( theo câu a)
nên chu vi ABC = 2 lần chu vi MNP =40cm

Ta gọi chu vi của hai tam giác ABC và MNP lần lượt là x, y.

Theo giả thiết, ta có: x y   =   2 5  và y - x = 51.

Từ đó tính được y = 85cm;  x = 34cm

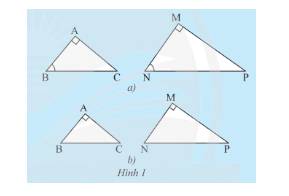
a) Xét tam giác \(ABC\) và tam giác \(MNP\) ta có:

\(\widehat B = \widehat N\) (giả thuyết)

\(\widehat A = \widehat M = 90^\circ \).

Do đó, \(\Delta ABC\backsim\Delta MNP\) (g.g)

b) Xét tam giác \(ABC\) và tam giác \(MNP\) ta có:

\(\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}}\) (giả thuyết)

\(\widehat A = \widehat M = 90^\circ \).

Do đó, \(\Delta ABC\backsim\Delta MNP\) (c.g.c).

Chọn A