Chủ đề / Chương

Bài học

Hãy tham gia nhóm Học sinh Hoc24OLM
Bạn chưa đăng nhập. Vui lòng đăng nhập để hỏi bài
Pham Trong Bach
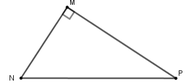
Cho tam giác MNP vuông tại M. Khi đó tan M N P ^ bằng: A. M N N P B.  M P N P C.  M N M...
Đọc tiếp
Lớp 9 Toán
Những câu hỏi liên quan
__Chucaheo__ _Con_

Tam giác MNP có MN = NP và góc M bằng 45ᵒ, khi đó kết luận nào sau đây là đúng nhất?

Tam giác MNP vuông tại M

Tam giác MNP đều

Tam giác MNP cân tại N

Tam giác MNP vuông cân tại N

Xem chi tiết
Lớp 7 Toán

Khách
 
TV Cuber
TV Cuber
25 tháng 3 2022 lúc 8:13

Tam giác MNP vuông cân tại N

Bình luận (0)
Kudo Shinichi AKIRA^_^
Kudo Shinichi AKIRA^_^
25 tháng 3 2022 lúc 8:13

Tam giác MNP vuông cân tại N

Bình luận (0)
ka nekk
ka nekk
25 tháng 3 2022 lúc 8:13

ý thứ tư đúng ko?

Bình luận (0)
Xem thêm câu trả lời
Pham Trong Bach
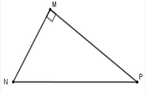
Cho tam giác MNP vuông tại M. Khi đó cos M N P ^ bằng: A. M N N P B.  M P N P C.   M N M...
Đọc tiếp
Xem chi tiết
Lớp 9 Toán

Khách
 
Cao Minh Tâm
Cao Minh Tâm
5 tháng 1 2020 lúc 10:30

Ta có: cos M N P ^ = M N N P

Đáp án cần chọn là: A

Bình luận (0)
Pham Trong Bach
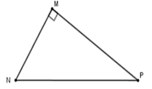
Cho tam giác MNP vuông tại M. Khi đó cos   M N P ^  bằng A.  M N N P B.  M P N P C.  M N M P...
Đọc tiếp
Xem chi tiết
Lớp 9 Toán

Khách
 
Cao Minh Tâm
Cao Minh Tâm
6 tháng 9 2017 lúc 2:49

Đáp án A

Bình luận (0)
NO NAME

Cho tam giác MNP vuông tại M có MN = 6 cm ,MP=8cm khi đó NP bằng:

a 🔼MNP vuông tại M                 b 🔼MNP vuông tại P

c 🔼MNP vuông tại N                  d 🔼MNP cân tại P

Xem chi tiết
Lớp 7 Toán

Khách
 
NGUYỄN♥️LINH.._.
NGUYỄN♥️LINH.._.
19 tháng 3 2022 lúc 17:09

A

Bình luận (0)
Ng Ngọc
Ng Ngọc
19 tháng 3 2022 lúc 17:09

A

Bình luận (0)
Mạnh=_=
Mạnh=_=
19 tháng 3 2022 lúc 17:09

A

Bình luận (0)
Xem thêm câu trả lời
Pham Trong Bach
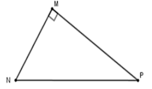
Cho tam giác MNP vuông tại M. Khi đó  cos M N P ^ bằng A.  M N N P B.  M P N P C.  M N M P D. ...
Đọc tiếp
Xem chi tiết
Lớp 9 Toán

Khách
 
Cao Minh Tâm
Cao Minh Tâm
28 tháng 1 2017 lúc 14:22

Đáp án A

Bình luận (0)
Nu Mùa

Bài 1 : cho tam giác ABC vuông tại A , AB = 6 , góc B = alpha, biết tan alpha bằng 5/2 . Tính : a, Cạnh AC b, Cạnh BC Bài 2 : Cho tam giác MNP vuông tại P . Hãy viết các tỉ số lượng giác của góc M và góc N . Biết góc M = 40° .

Xem chi tiết
Lớp 9 Toán

Khách
 
HT.Phong (9A5)
HT.Phong (9A5) CTV
6 tháng 10 2023 lúc 18:59

Bài 1:

a) Ta có:

\(tanB=\dfrac{AC}{AB}\Rightarrow\dfrac{AC}{AB}=\dfrac{5}{2}\)

\(\Rightarrow AC=\dfrac{AB\cdot5}{2}=\dfrac{6\cdot5}{2}=15\)  

b) Áp dụng Py-ta-go ta có: 

\(BC^2=AB^2+AC^2=6^2+15^2=261\)

\(\Rightarrow BC=\sqrt{261}=3\sqrt{29}\)

Bình luận (0)
HT.Phong (9A5)
HT.Phong (9A5) CTV
6 tháng 10 2023 lúc 19:02

Bài 2: 

\(\left\{{}\begin{matrix}sinM=sin40^o\approx0,64\Rightarrow cosN\approx0,64\\cosM=cos40^o\approx0,77\Rightarrow sinN\approx0,77\\tanM=tan40^o\approx0,84\Rightarrow cotN\approx0,84\\cotM=cot40^o\approx1,19\Rightarrow tanN\approx1,19\end{matrix}\right.\)

Bình luận (0)
Trần Minh Nguyệt

cho đường tròn tâm (O;R) ngoại tiếp tam giác MNP vuông cân tại M khi đó MN bằng ?

Xem chi tiết
Lớp 9 Toán Bài 4: Một số hệ thức về cạnh và góc trong tam giá...

Khách
 
NO NAME

cho tam giác MNP vuông tại M có MN = 6 cm,MP=8 cm .khi đó NP bằng 

A. 100cm     B.10cm         C.14cm       D.48cm

Xem chi tiết
Lớp 6 Toán

Khách
 
Good boy
Good boy
19 tháng 3 2022 lúc 20:24

B

Bình luận (2)
Mạnh=_=
Mạnh=_=
19 tháng 3 2022 lúc 20:24

B

Bình luận (0)
kodo sinichi
kodo sinichi CTV
19 tháng 3 2022 lúc 20:24

B

Bình luận (0)
Xem thêm câu trả lời
11 Vũ Thị Hồng Hà

Cho tam giác MNP vuông cân tại M có NP= căn bậc 2 của 32 cm, khi đó độ dài cạnh MN bằng:

Xem chi tiết
Lớp 7 Toán

Khách
 
☆Châuuu~~~(๑╹ω╹๑ )☆
☆Châuuu~~~(๑╹ω╹๑ )☆
22 tháng 3 2022 lúc 17:46

Ta có 

\(NP=\sqrt{32}=4\sqrt{2}cm\)

Mà \(\Delta MNP\) vuông cân 

\(\Rightarrow MN=NP\)

Áp dụng định lí Pytago ta có

\(NP^2=NM^2+MP^2\\ mà.MN=NP\\ \Rightarrow MN=\dfrac{NP}{2}=.....\)

Bình luận (0)