Cho ΔABC, AD là phân giác trong của góc A. Hãy chọn câu đúng:
A. D C D B = A B A C
B. A B D B = A C D C
C. A B D B = D C A C
D. A D D B = A C A D
Những câu hỏi liên quan
19 tháng 4 2022 lúc 12:50
Bài 5: Cho ΔABC có A^ 120°. Các đường phân giác AD, BE . Tính số đo góc A. 55° B. 45° C. 60° D. 30°Bài 7: Em hãy chọn câu đúng nhấtA. Ba tia phân giác của tam giác cùng đi qua một điểm, điểm đó gọi là trọng tâm của tam giácB. Giao điểm ba đường phân giác của tam giác cách đều ba cạnh của tam giácC. Trong một tam giác, đường trung tuyến xuất phát từ một đỉnh đồng thời là đường phân giác ứng với cạnh đáyD. Giao điểm ba đường phân giác của tam giác là tâm đường tr...
Đọc tiếp
Bài 5: Cho ΔABC có A^ = 120°. Các đường phân giác AD, BE . Tính số đo góc 
A. 55° B. 45° C. 60° D. 30°
Bài 7: Em hãy chọn câu đúng nhất
A. Ba tia phân giác của tam giác cùng đi qua một điểm, điểm đó gọi là trọng tâm của tam giác
B. Giao điểm ba đường phân giác của tam giác cách đều ba cạnh của tam giác
C. Trong một tam giác, đường trung tuyến xuất phát từ một đỉnh đồng thời là đường phân giác ứng với cạnh đáy
D. Giao điểm ba đường phân giác của tam giác là tâm đường tròn ngoại tiếp tam giác đó
Xem thêm câu trả lời
Cho ΔABC, AD là phân giác trong của góc A. Hãy chọn câu sai: A.
D
C
D
B
A
C
A
B
B.
A
B
D
B
A
C
D...
Đọc tiếp
Cho ΔABC, AD là phân giác trong của góc A. Hãy chọn câu sai:
A. D C D B = A C A B
B. A B D B = A C D C
C. A B D B = D C A C
D. D B A B = D C A C
Vì AD là phân giác góc B A C ^ nên ta có: B D D C = A B A C (tính chất đường phân giác của tam giác).
⇒ A B D B = A C D C hay B đúng
Lại có: B D D C = A B A C => D C B D = A C A B nên A đúng
B D D C = A B A C => D B A B = D C A C nên D đúng
Chỉ có C sai
Đáp án: C
Đúng 0
Bình luận (0)
Cho ΔABC, AE là phân giác ngoài của góc A. Hãy chọn câu đúng: A.
A
B
A
E
B
E
C
E
B.
A
E
A
C
B
E
C...
Đọc tiếp
Cho ΔABC, AE là phân giác ngoài của góc A. Hãy chọn câu đúng:
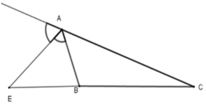
A. A B A E = B E C E
B. A E A C = B E C E
C. A B A C = C E B E
D. A B A C = B E C E
Vì trong tam giác, đường phân giác của một góc chia cạnh đối diện thanh hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy nên A B A C = B E C E
Đáp án D
Đúng 0
Bình luận (0)
1) cho ΔABC đều có cạnh 3ma) tính diện tích ΔABCb) lấy M nằm trong tam giác ABC. vẽ MI, MJ, MK lần lượt vuông góc với AB,AC,BC. hãy tính MI+MJ+MK2) cho ΔABC. hạ AD vuông góc với đường phân giác trong của góc B tại D, hạ AE vuông góc với đường phân giác ngoài của goác B tại E. a) c/m tứ giác ADBE là hình chữ nhật.b) tìm điều kiện của ΔABC để tứ giác ADBE là hình vuông.c) c/m DE//BC
Đọc tiếp
1) cho ΔABC đều có cạnh =3m
a) tính diện tích ΔABC
b) lấy M nằm trong tam giác ABC. vẽ MI, MJ, MK lần lượt vuông góc với AB,AC,BC. hãy tính MI+MJ+MK
2) cho ΔABC. hạ AD vuông góc với đường phân giác trong của góc B tại D, hạ AE vuông góc với đường phân giác ngoài của goác B tại E.
a) c/m tứ giác ADBE là hình chữ nhật.
b) tìm điều kiện của ΔABC để tứ giác ADBE là hình vuông.
c) c/m DE//BC
a. hạ đương cao AK
suy ra BK=KC=3:2=1.5(cm)
Xét tam giac ABC có góc AKB=90
AK^2+BK^2=AB^2(đl py-ta-go)
AK=\(\dfrac{3\sqrt{3}}{2}\)
SABC=\(\dfrac{1}{2}.\dfrac{3\sqrt{3}}{2}.3=\dfrac{9\sqrt{3}}{4}\)
Đúng 0
Bình luận (0)
Cho ΔABC, AE là phân giác ngoài của góc A. Hãy chọn câu sai: A.
C
E
A
C
B
E
A
B
B.
A
B
C
E
A
C
B...
Đọc tiếp
Cho ΔABC, AE là phân giác ngoài của góc A. Hãy chọn câu sai:
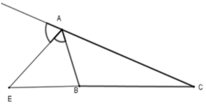
A. C E A C = B E A B
B. A B C E = A C B E
C. A B B E = A C C E
D. A B A C = B E C E
Vì trong tam giác, đường phân giác của một góc chia cạnh đối diện thanh hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy nên A B A C = B E C E
A B A C = B E C E ⇒ A B B E = A C C E nên C đúng
A B B E = A C C E ⇒ C E A C = B E A B nên A đúng
Chỉ có B sai.
Đáp án: B
Đúng 0
Bình luận (0)
Khi nào ta kết luận được tia Ot là tia phân giác của góc xOy ?Trong những câu trả lời sau em hãy chọn câu trả lời đúng: Tia Ot là tia phân giác của góc xOy khia)
x
O
t
^
y
O
t
^
b)
x
O
t
^
+
t...
Đọc tiếp
Khi nào ta kết luận được tia Ot là tia phân giác của góc xOy ?
Trong những câu trả lời sau em hãy chọn câu trả lời đúng: Tia Ot là tia phân giác của góc xOy khi
a) x O t ^ = y O t ^
b) x O t ^ + t O y ^ = x O y ^
c) x O t ^ + t O y ^ = x O y ^ và x O t ^ = y O t ^
d) x O t ^ = y O t ^ = x O y ^ 2
Chọn đáp án C và D. Thỏa mãn 2 điều kiện chứng minh một tia là tia phân giác là : Tia nằm giữa và tạo với hai cạnh hai góc bằng nhau.
Đúng 0
Bình luận (0)
Cho ΔABC , góc A =90 độ , góc B=60độ .
a, So sánh AD và BD
b, Trên BC lấy D sao cho BD=AB . Qua D dựng đường vuông góc với BC cắt tia đối của AB tại E . Chứng minh : ΔABC=ΔDBE
c, H là giao điểm của AC và ED . Chứng minh : BH là phân giác của góc ABC
d, Qua B vẽ đường thẳng vuông góc AB cắt ED tại K . Chứng minh : ΔHBK đều
b) Xét ΔABC vuông tại A và ΔDBE vuông tại D có
AB=BD(gt)
\(\widehat{ABC}\) chung
Do đó: ΔABC=ΔDBE(cạnh góc vuông-góc nhọn kề)
c) Xét ΔBAH vuông tại A và ΔBDH vuông tại D có
BH chung
BA=BD(gt)
Do đó: ΔBAH=ΔBDH(Cạnh huyền-cạnh góc vuông)
Suy ra: \(\widehat{ABH}=\widehat{DBH}\)(hai góc tương ứng)
hay BH là tia phân giác của \(\widehat{ABC}\)
d) Ta có: BH là tia phân giác của \(\widehat{ABC}\)(cmt)
nên \(\widehat{ABH}=\dfrac{\widehat{ABC}}{2}=\dfrac{60^0}{2}=30^0\)
Ta có: \(\widehat{ABH}+\widehat{HBK}=90^0\)
\(\Leftrightarrow\widehat{HBK}+30^0=90^0\)
hay \(\widehat{HBK}=60^0\)
Xét ΔCHD vuông tại D và ΔCBA vuông tại A có
\(\widehat{ACB}\) chung
Do đó: ΔCHD\(\sim\)ΔCBA(g-g)
Suy ra: \(\widehat{CHD}=\widehat{CBA}\)(hai góc tương ứng)
\(\Leftrightarrow\widehat{CHD}=60^0\)
mà \(\widehat{CHD}=\widehat{HKB}\)(hai góc so le trong, BK//AC)
nên \(\widehat{HKB}=60^0\)
Xét ΔHBK có
\(\widehat{HKB}=60^0\)(cmt)
\(\widehat{HBK}=60^0\)(cmt)
Do đó: ΔHBK đều(Dấu hiệu nhận biết tam giác đều)
Đúng 0
Bình luận (1)
Câu hỏi: Cho ΔABC, có góc B = góc C. Tia phân giác của góc A cắt BC tại D.
a. Chứng minh: ΔADB = ΔADC.
b. Chứng minh: AB = AC.
c. Chứng minh: AD là đường trung trực của BC.
a) Xét \(\Delta ADB\) và \(\Delta ADC\) ta có:
\(\widehat{BAD}+\widehat{B}+\widehat{BDA}=180^o\)
\(\widehat{DAC}+\widehat{C}+\widehat{CDA}=180^o\)
Mà \(\widehat{B}=\widehat{C}\left(gt\right)\)(*)
\(\widehat{BAD}=\widehat{DAC}\) (AD là phân giác)
\(\Rightarrow\widehat{BDA}=\widehat{CDA}\) (**)
AD là cạnh chung. (***)
Vậy: từ (*) (**) (***) ta có \(\Delta ADB\) = \(\Delta ADC\) (g.c.g)
b) Vì: \(\Delta ADB\) = \(\Delta ADC\) (cm a)
\(\Rightarrow AB=AC\) (2 cạnh tương ứng)
c) Vì: \(\Delta ADB\) = \(\Delta ADC\) (cm a)
\(\Rightarrow DB=DC\) (2 cạnh tương ưng)
Mà D thuộc BC (gt)
=> D là trung điểm của BC. (****)
Lại có: AD là tia phân giác góc A (*****)
Từ (****) và (*****) suy ra AD là đường trung trực của BC
Đúng 0
Bình luận (0)
Cho tam giác ABC có B ^ = C ^ . Tia phân giác của góc A cắt BC tại D. Chọn câu đúng:
A. BD = DC
B. AB = AC
C. Cả A và B đều đúng
D. A đúng, B sai
