Cho ba số thực dương a; b và c thỏa mãn :\(a+b+c=3\). Tìm giá trị lớn nhất của biểu thức sau:
\(P=\sqrt{9a+16b}+\sqrt{9b+16c}+\sqrt{9c+16a}\)
Những câu hỏi liên quan
Cho a, b, c là ba số thực dương, khác 1. Mệnh đề nào dưới đây đúng A.
log
a
b
a
3
log
a
b
−
3
B.
log
a
α
b
α
l...
Đọc tiếp
Cho a, b, c là ba số thực dương, khác 1. Mệnh đề nào dưới đây đúng
A. log a b a 3 = log a b − 3
B. log a α b = α log a b
C. a log b c = b
D. log a b = log b c . log c a
Đáp án A
Phương pháp giải: Áp dụng các công thức cơ bản của biểu thức chứa lôgarit
Lời giải:
Ta có: log a b a 3 = log a b − log a a 3 = log a b − 3 và
log a α b = 1 α log a b
Đúng 0
Bình luận (0)
Cho a, b, c là ba số thực dương, khác 1. Mệnh đề nào dưới đây đúng
Cho a; b; c là ba số thực dương, khác 1. Mệnh đề nào dưới đây sai? A.
log
b
a
log
b
c
.
log
c
a
B.
log
a
α
b
1
α
log...
Đọc tiếp
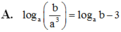
Cho a; b; c là ba số thực dương, khác 1. Mệnh đề nào dưới đây sai?
A. log b a = log b c . log c a
B. log a α b = 1 α log a b
C. log a b a 3 = log a b 3
D. a log a b = b
Cho ba số thực dương a,b,c khác 1. Đồ thị các hàm số
y
log
a
x
,
y
log
b
x
,
y
log
c
x
cho như hình vẽ A.
b
c
1
a
B.
b
a
1
c...
Đọc tiếp
Cho ba số thực dương a,b,c khác 1. Đồ thị các hàm số y = log a x , y = log b x , y = log c x cho như hình vẽ
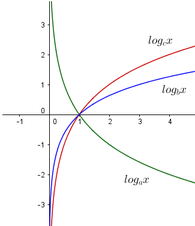
A. b > c > 1 > a
B. b > a > 1 > c
C. a > c > 1 > b
D. c > b > 1 > a
Cho số thực x lớn hơn 1 và ba số thực dương a, b, c khác 1 thỏa mãn điều kiện
log
a
x
log
b
x
0
log
c
x
. Mệnh đề nào sau đây đúng ? A. c a b B. b a c C. c b a D. a b c
Đọc tiếp
Cho số thực x lớn hơn 1 và ba số thực dương a, b, c khác 1 thỏa mãn điều kiện log a x > log b x > 0 > log c x . Mệnh đề nào sau đây đúng ?
A. c > a > b
B. b > a > c
C. c > b > a
D. a > b > c
Đáp án B
Ta có:
log a x > log b x > 0 > log c x ⇔ 1 log x a > 1 log x b > 0 log x c < 0 ⇔ log x b > log x c > 0 c < 1 ⇔ b > a > 1 > c .
Đúng 0
Bình luận (0)
Cho ba số thực dương a,b,c .Chứng minh rằng :
\(1+\dfrac{3}{ab+bc+ca}\ge\dfrac{6}{a+b+c}\)
\(1+\dfrac{9}{3\left(ab+bc+ca\right)}\ge1+\dfrac{9}{\left(a+b+c\right)^2}\ge2\sqrt{\dfrac{9}{\left(a+b+c\right)^2}}=\dfrac{6}{a+b+c}\)
Đúng 1
Bình luận (0)
Cho ba số thực dương: a, b, c
≤
1 thỏa mãn:
a
1
-
b
2
+
b
1
-
c
2
+
c
1
-
a...
Đọc tiếp
Cho ba số thực dương: a, b, c ≤ 1 thỏa mãn: a 1 - b 2 + b 1 - c 2 + c 1 - a 2 = 3 2 . Chọn câu đúng.
A. a 2 + b 2 + c 2 = 3 2
B. a 2 + b 2 + c 2 = 3
C. a 2 + b 2 + c 2 = 1 2
D. a 2 + b 2 + c 2 = 2 3
Cho ba số thực dương a,b,c thỏa mãn Tìm giá trị lớn nhất của biểu thức P
Áp dụng BĐT Bun nhia cốp xki :
\(\left(9a^3+3b^2+c\right)\left(\frac{1}{9a}+\frac{1}{3}+c\right)\ge\left(a+b+c\right)^2=1\)
<=>\(\frac{1}{9a^3+3b^2+c}\le\frac{1}{9a}+\frac{1}{3}+c\Leftrightarrow\frac{a}{9a^3+3b^2+c}\le a\left(\frac{1}{9a}+\frac{1}{3}+c\right)\)
<=> \(\frac{a}{9a^3+3b^2+c}\le\frac{1}{9}+\frac{1}{3}a+ac\)
Làm tương tự với 2 cái còn lại
CỘng vế với vế ba BĐT => GTLN
Đúng 0
Bình luận (0)
tại sao
$\left(9a^3+3b^2+c\right)\left(\frac{1}{9a}+\frac{1}{3}+c\right)\ge \left(a+b+c\right)^2=1$
Đúng 0
Bình luận (0)
Thì bđt bunhia ấy
Cho số thực x lớn hơn 1 và ba số thực dương a, b, c khác 1 thỏa mãn điều kiện loga x logb x logc x. Mệnh đề nào sau đây đúng ? A. c a b B. b a c C. c b a D. a b c
Đọc tiếp
Cho số thực x lớn hơn 1 và ba số thực dương a, b, c khác 1 thỏa mãn điều kiện loga x > logb x > logc x. Mệnh đề nào sau đây đúng ?
A. c > a > b
B. b > a > c
C. c > b > a
D. a > b > c
Cho ba số thực dương ............ ( ** ).
An nhận nè em.
Gọi vế trái của ( ** ) là T, ta có:
\(T=\frac{m}{2}\left(Y+Y+X\right)+\left(n-\frac{m}{2}\right)X\)
Với \(X=\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\), \(Y=a+b+c\), theo bài toán 1 ta có \(X\ge3\);\(XY^2\ge27\).
Suy ra:
\(T\ge\frac{m}{2}.3\sqrt[3]{XY^2}+\left(n-\frac{m}{n}\right).3\)( do \(2n\ge m\))
\(\ge\frac{9m}{2}+3\left(n-\frac{m}{n}\right)=3\left(m+n\right)\)
Đẳng thức xảy ra khi và chỉ khi a = b = c = 1.
Đúng 0
Bình luận (0)
coi 3 số là a,b,c =>a=b=c=1
tich ủng hộ nhé
Đúng 0
Bình luận (0)