Cho hình lăng trụ đều ABC. A’B’C’ có cạnh đáy bằng 2a, cạnh bên bằng a. Tính góc giữa hai mặt phẳng (AB’C’) và (A’B’C’).
A. π 6
B. π 3
C. arccos 3 4
D. arcsin 3 4
Cho lăng trụ đều ABC.A’B’C’ có cạnh đáy bằng a, cạnh bên bằng a 2 . Tính góc giữa mặt phẳng (AB’C’) và (A’B’C’).
A. arctan 3 4
B. 30 0
C. 45 0
D. arc cos 3 4
Cho hình lăng trụ ABC.A’B’C’ có tất cả các cạnh đều bằng a. Góc tạo bởi cạnh bên và mặt phẳng đáy bằng 300. Hình chiếu H của A trên mặt phẳng (A’B’C’) là trung điểm của B’C’. Tính theo a khoảng cách giữa hai mặt phẳng đáy của lăng trụ ABC.A’B’C’.
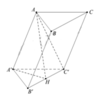
A. a 2
B. a 3
C. a 3 2
D. a 2 2
Đáp án A
Khoảng cách giữa hai mặt đáy là h = AH = A’H.tan A A ' H ^ = a 3 2 . tan 30 0 = a 2
Cho lăng trụ tam giác ABC.A’B’C’ có đáy là tam giác đều cạnh a.Hình chiếu của đỉnh A’ xuống mặt phẳng (ABC) trùng với trung điểm của cạnh BC.Biết góc giữa cạnh bên và mặt đáy bằng 60 độ.Tính khoảng cách giữa hai mặt phẳng (ABC) và (A’B’C’).
Cho hình lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy bằng a và cạnh bên bằng 2a Một hình trụ có hai đáy là hai hình tròn ngoại tiếp hai tam giác ABC và A’B’C’ Diện tích xung quanh của hình trụ bằng
A. 4 3 π a 2 3
B. 2 3 π a 2 3
C. 4 π a 2
D. 2 π a 2
Cho lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, cạnh bên tạo với mặt phẳng bằng 45°. Hình chiếu của A trên mặt phẳng (A’B’C’) trùng với trung điểm của A’B’. Tính thể tích V của khối lăng trụ theo a.
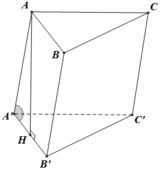
A. V = a 3 3 2
B. V = a 3 3 8
C. V = a 3 3 16
D. V = a 3 3 24
Cho hình lăng trụ đều ABC.A’B’C’ có đáy là tam giác đều cạnh 2, cạnh bên bằng 1. Góc giữa hai mặt phẳng (A’BC) và (AB’C’) bằng
A. 60 °
B. 90 °
C. 30 °
D. 45 °
Cho lăng trụ tam giác ABC. A’B’C’ có đáy là tam giác đều cạnh a. Độ dài cạnh bên bằng 4a. Mặt phẳng (BCC’B’) vuông góc với đáy và B ' B C ^ = 30 0 .Thể tích khối chóp A. CC’B’ là
A. a 3 3 2
B. a 3 3 12
C. a 3 3 18
D. a 3 3 6
Cho lăng trụ ABC.A’B’C’có AB = 2a, BC = 2a, góc A’B’C’ = 120 0 . Hình chiếu vuông góc của A trên mặt phẳng (A’B’C’) trung với điểm của A’B’. Góc giữa đường thẳng AC’ và mặt phẳng (A’B’C’) bằng 60 0 . Gọi α là góc giữa hai mặt phẳng (BCC’B’) và (ABC). Khi đó, tan α có giá trị là:
A. 21
B. 2 2
C. 21 2
D. 2 21
Đáp án D
Phương pháp: Cho hai mặt phẳng (α) và (β) cắt nhau, ta xác định góc giữa (α) và (β) như sau:
- Tìm giao tuyến ∆ của hai mặt phẳng (α) và (β).
- Tìm trong mỗi mặt phẳng (α), (β) một đường thẳng 𝑎, cùng cùng vuông góc với ∆ và cùng cắt ∆ tại điểm .
- Xác định góc giữa 𝑎 và 𝑏.
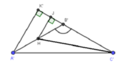
Cách giải: Gọi H là trung điểm của A’B’ => AH ⊥ (A’B’C’)
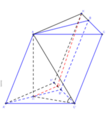
Kẻ HJ, A'K' ⊥ B'C', (J, K' ∈ B'C'), AK ⊥ BC, (K ∈ BC)
HJ//A'K', A'K'//AK => HJ//AK => H,J,A,K đồng phẳng
Vì 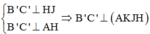
Ta có: 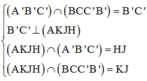
=> ((BCC'B');(A'B'C')) = (KJ;HJ)
A ' B ' K ' ^ = 180 0 - 120 0 = 60 0
=> A'K' = A'B' . sin 60 0
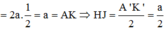
Xét ∆B’HC’ : H'C = ![]()
![]()
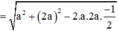
![]()
∆AHC’ vuông tại H => AH = HC.tanC’ = HC.tan(AC’;(A’B’C’)) (vì AH ⊥ (A’B’C’))
![]()
Xét hình thang vuông AKJH:
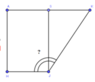

Kẻ ![]()
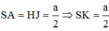
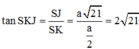
Vì AK//HJ
![]()
![]()
Cho hình lăng trụ đều ABC. A’B’C’ biết góc giữa hai mặt phẳng (A’BC) và (ABC) bằng 45 0 , diện tích tam giác A’BC bằng a 2 6 . Tính diện tích xung quanh của hình trụ ngoại tiếp hình lăng trụ ABC. A’B’C’
A. 4 πa 2 3 3
B. 2 πa 2
C. 4 πa 2
D. 8 πa 2 3 3