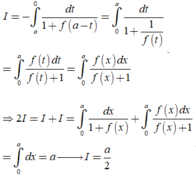Cho hàm số y = f (x) thỏa mãn f(0) = 1, f'(x) liên tục trên R và ∫ 0 3 f ' ( x ) dx = 9 .Giá trị của f(3) là

A. 6

B. 3

C. 10

D. 9

Cho hàm số y = f (x) thỏa mãn f(0) = 1, f'(x) liên tục trên R và ∫ 0 3 f ' ( x ) d x = 9  . Giá trị của f(3) là

Cho hàm số f(x) liên tục trên R và F(x) là một nguyên hàm của f(x), biết  ∫ 0 9 f x d x = 9  và F(0) = 9.

A. F(9) = -3

B. F(9) = -12.

C. F(9) = 12.

D. F(9) = 6.

Cho hàm số f(x) liên tục trên R và F(x) là một nguyên hàm của f(x) biết ∫ 0 9 f x d x = 9  và F(0)=9

A. F(9) = -3

B. F(9) = -12

C. F(9) = 12

D. F(9) = 6

Cho hàm số y = f(x) xác định và liên tục trên R \ 0 biết x . f x ≠ - 1 ∀ x ≠ 0 f(1) = -2 và  với ∀ x ∈ R \ 0 Tính  ∫ 1 e f x d x

A. .

B. .

C. .

D. .

Cho hàm số f(x) xác định và liên tục trên R và có đạo hàm f'(x) thỏa mãn f ' ( x ) = ( 1 - x ) ( x + 2 ) g ( x ) + 2018  với g ( x ) < 0 , ∀ x ∈ R . Hàm số y = f ( 1 - x ) + 2018 x + 2019  nghịch biến trên khoảng nào dưới đây?

A .   ( 1 ; + ∞ ) .

B .   ( 0 ; 3 ) .

C .   ( - ∞ ; 3 ) .

D .   ( 4 ; + ∞ ) .

Cho hàm số y=f(x) liên tục, không âm trên R thỏa mãn f ( x ) . f ' ( x ) = 2 x f ( x ) 2 + 1  và f(0)=0. Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y=f(x) trên đoạn [1;3] lần lượt là:

A. M=20;m=2

B.  M = 4 11 ;   m = 3

C.  M = 20 ;   m = 2

D.  M = 3 11 ;   m = 3

Cho hàm số  y = f ( x ) xác định và liên tục trên R thỏa mãn f ( x ) > 0 , f ’ ( x ) = - e x . f 2 ( x ) , ∀ x ∈ R và f ( 0 ) = 1 2 . Tính giá trị của  f ( ln 2 )

A.  ln 2 + 1 2

B.  1 4

C.  1 3

D.  ln 2 2 + 1 2

Cho hàm số y = f(x) liên tục trên R và a > 0. Giả sử rằng với mọi  x ∈ 0 ; a , ta có f(x) > 0 và f(x)f(a – x) = 1. Tính I = ∫ 0 a d x 1 + f ( x ) .

A. a 2 .

B. 2a.

C. a 3 .

D. aln(a + 1).