Cho hình lăng trụ đứng ABCD.A’B’C’D’, với mặt đáy ABCD là hình chữ nhật. Khi đó:
A. AA’ = CD’
B. BC’ = CD’
C. AC’ = BB’
D. AA’ = CC’
Những câu hỏi liên quan
Cho hình lăng trụ đứng ABCD.A’B’C’D’ có đáy là hình thang vuông ABCD vuông tại A, B (AB // BC) và BC 12cm, AD 16cm, CD 5cm, đường cao AA’ 6cm. Thể tích của hình lăng trụ là A. 200
c
m
3
B. 250
c
m
3
C. 252
c
m
3
D. 410
c
m
3
Đọc tiếp
Cho hình lăng trụ đứng ABCD.A’B’C’D’ có đáy là hình thang vuông ABCD vuông tại A, B (AB // BC) và BC = 12cm, AD = 16cm, CD = 5cm, đường cao AA’ = 6cm. Thể tích của hình lăng trụ là
A. 200 c m 3
B. 250 c m 3
C. 252 c m 3
D. 410 c m 3
Cho hình lăng trụ đều ABCD.A’B’C’D’ có đáy là hình vuông cạnh a. Mặt phẳng (α) lần lượt cắt các cạnh bên AA’, BB’, CC’ tại 4 điểm M, N, P, Q. Góc giữa mặt phẳng (α) và mặt phẳng (ABCD) là 600. Diện tích tứ giác MNPQ là : A.
2
3
a
2
B.
1
2...
Đọc tiếp
Cho hình lăng trụ đều ABCD.A’B’C’D’ có đáy là hình vuông cạnh a. Mặt phẳng (α) lần lượt cắt các cạnh bên AA’, BB’, CC’ tại 4 điểm M, N, P, Q. Góc giữa mặt phẳng (α) và mặt phẳng (ABCD) là 600. Diện tích tứ giác MNPQ là :
A. 2 3 a 2
B. 1 2 a 2
C. 2 a 2
D. 3 2 a 2
Đáp án C
Phương pháp : Sử dụng công thức 
Cách giải :
Đúng 0
Bình luận (0)
Cho hình lăng trụ đứng ABCD.A’B’C’D’ có đáy là hình thoi, biết AA’4a, AC2a, BDa. Thể tích của khối lăng trụ là: A. 2a3 B. 8a3 C. 6a3 D. 4a3.
Đọc tiếp
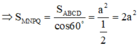
Cho hình lăng trụ đứng ABCD.A’B’C’D’ có đáy là hình thoi, biết AA’=4a, AC=2a, BD=a. Thể tích của khối lăng trụ là:
A. 2a3
B. 8a3
C. 6a3
D. 4a3.
Cho hình lăng trụ đứng ABCD.A’B’C’D’ có đáy là hình thoi, biết AA’ 4a; AC 2a, BD a. Thế tích V của khối lăng trụ là A.
V
2
a
3
B.
V
4
a
3
C.
V
8
3
a
3
D.
V
8
a
3
Đọc tiếp
Cho hình lăng trụ đứng ABCD.A’B’C’D’ có đáy là hình thoi, biết AA’ = 4a; AC = 2a, BD = a. Thế tích V của khối lăng trụ là
A. V = 2 a 3
B. V = 4 a 3
C. V = 8 3 a 3
D. V = 8 a 3
Phương pháp
Thể tích khối lăng trụ có diện tích đáy S và chiều cao h: V = Sh.
Công thức tính diện tích hình thoi ABCD là: S A B C D = 1 2 A B C D .
Cách giải
Đúng 0
Bình luận (0)
Cho hình lăng trụ đứng ABCD.A’B’C’D’ có đáy là hình thoi, biết AA’ 4a; AC 2a, BD a. Thế tích V của khối lăng trụ là
Đọc tiếp
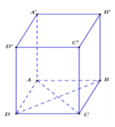
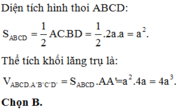
Cho hình lăng trụ đứng ABCD.A’B’C’D’ có đáy là hình thoi, biết AA’ = 4a; AC = 2a, BD = a. Thế tích V của khối lăng trụ là
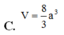
Cho hình lăng trụ đứng ABCD.A’B’C’D’ có đáy là hình thoi, biết AA’=4a, AC=2a, BD=a. Thể tích V của khối lăng trụ là
A. 8 a 3
B. 2 a 3
C. 8 3 a 3
D. 4 a 3
1. Cho hình chữ nhật ABCD. Vẽ AH vuông góc BD (H thuộc BD), HK // CD (K thuộc BC).a) Chứng minh tam giác ADH đồng dạng với tam giác DBC.b/ Chứng minh CD.BK AH.BH.c/ Cho biết AB5cm, HB-4cm. Tính BK?2. Cho hình lăng trụ đứng ABC.ABC có đáy là tam giác cân ở A, AB5cm. BC6cm và AA 7cm. Gọi M, M lần lượt là trung điểm của BC và BC.a/ Chứng minh MM song song với mặt phẳng ABBAb/ Tính thể tích của hình lăng trụ đứng trên.
Đọc tiếp
1. Cho hình chữ nhật ABCD. Vẽ AH vuông góc BD (H thuộc BD), HK // CD (K thuộc BC).
a) Chứng minh tam giác ADH đồng dạng với tam giác DBC.
b/ Chứng minh CD.BK = AH.BH.
c/ Cho biết AB=5cm, HB-4cm. Tính BK?
2. Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác cân ở A, AB=5cm. BC=6cm và AA' = 7cm. Gọi M, M' lần lượt là trung điểm của BC và BC.
a/ Chứng minh MM' song song với mặt phẳng ABB'A'
b/ Tính thể tích của hình lăng trụ đứng trên.
SGK Chân trời sáng tạo
20 tháng 8 2023 lúc 21:10
Cho hình lăng trụ đứng \(ABCD.A'B'C'D'\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(B\), \(AA' = 2a,AD = 2a,AB = BC = a\).
a) Tính độ dài đoạn thẳng \(AC'\).
b) Tính tổng diện tích các mặt của hình lăng trụ.
a) \(\Delta ABC\) vuông cân tại \(B \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \)
\(CC' = AA' = 2a\)
\(CC' \bot \left( {ABCD} \right) \Rightarrow CC' \bot AC\)
\( \Rightarrow \Delta ACC'\) vuông tại \(C \Rightarrow AC' = \sqrt {A{C^2} + CC{'^2}} = a\sqrt 6 \)
b) \({S_{ABC{\rm{D}}}} = {S_{A'B'C'C'}} = \frac{1}{2}\left( {A{\rm{D}} + BC} \right).AB = \frac{{3{a^2}}}{2}\)
Gọi \(M\) là trung điểm của \(AD\)
\( \Rightarrow ABCM\) là hình vuông\( \Rightarrow MC = M{\rm{D}} = MA = \frac{1}{2}A{\rm{D}} = a\)
\(\Delta MC{\rm{D}}\) vuông cân tại \(M \Rightarrow C{\rm{D}} = \sqrt {C{M^2} + D{M^2}} = a\sqrt 2 \)
\(\begin{array}{l}{S_{ABB'A'}} = AB.AA' = 2{a^2}\\{S_{ADD'A'}} = AD.AA' = 4{a^2}\\{S_{BCC'B'}} = BC.CC' = 2{a^2}\\{S_{C{\rm{DD}}'{\rm{C}}'}} = C{\rm{D}}.CC' = 2{a^2}\sqrt 2 \end{array}\)
Tổng diện tích các mặt của hình lăng trụ là:
\(\begin{array}{l}S = {S_{ABC{\rm{D}}}} + {S_{A'B'C'C'}} + {S_{ABB'A'}} + {S_{ADD'A'}} + {S_{BCC'B'}} + {S_{C{\rm{DD}}'{\rm{C}}'}}\\ & = \frac{{3{a^2}}}{2} + \frac{{3{a^2}}}{2} + 2{a^2} + 4{a^2} + 2{a^2} + 2{a^2}\sqrt 2 = \left( {11 + 2\sqrt 2 } \right){a^2}\end{array}\)
Đúng 0
Bình luận (0)
Một nhà kho có dạng khói hộp chữ nhật đứng ABCD.A’B’C’D’, nền là hình chữ nhật ABCD có AB 3m, BC 6m, chiều cao AA’ 3m, chắp thêm một lăng trụ tam giác đều mà một mặt bên là A’B’C’D’ và A’B’ là một cạnh đyá của lăng trụ. Tính thể tích của nhà kho? A.
9
12
+
3
2
m
3
B. ...
Đọc tiếp
Một nhà kho có dạng khói hộp chữ nhật đứng ABCD.A’B’C’D’, nền là hình chữ nhật ABCD có AB = 3m, BC = 6m, chiều cao AA’ = 3m, chắp thêm một lăng trụ tam giác đều mà một mặt bên là A’B’C’D’ và A’B’ là một cạnh đyá của lăng trụ. Tính thể tích của nhà kho?
A. 9 12 + 3 2 m 3
B. 27 4 + 3 2 m 3
C. 54 m 3
D. 27 3 2 m 3
