Chọn khẳng định đúng. Nếu phương trình a x 2 = m . x + n có hai nghiệm phân biệt thì đường thẳng d: y = mx + n và parabol (P): y = a x 2
A. Cắt nhau tại hai điểm
B. Tiếp xúc với nhau
C. Không cắt nhau
D. Cắt nhau tại gốc tọa độ
Cho phương trình có tham số m:
2 m + 1 x - m x - 1 = x + m . (*)
Chọn khẳng định đúng trong các khẳng định sau:
A. Phương trình luôn có hai nghiệm phân biệt
B. Khi m ≠ - 2 thì phương trình có hai nghiệm phân biệt
C. Khi m ≠ - 1 thì phương trình có hai nghiệm phân biệt
D. Khi m ≠ - 1 và m ≠ - 2 thì phương trình có hai nghiệm phân biệt
Trước hết phải chú ý điều kiện xác định của phương trình là x ≠ 1 .
Ta có: 2 m + 1 x - m x - 1 = x + m
Suy ra: (2m + 1) x- m = (x+ m). (x- 1)
⇔ 2 m x + x - m = x 2 - x + m x - m ⇔ x 2 - 2 x - m x = 0 ⇔ x 2 - 2 + m x = 0 ⇔ x x - 2 + m = 0 ⇔ [ x = 0 x = 2 + m
Khi m = 2 thì hai nghiệm bằng nhau đều bằng 0.
Khi m = -1 thì x = 1 ( không thỏa mãn điều kiện) nên không phải là nghiệm.
Vì vậy các phương án A B, C sai. Đáp án là D.
Cho phương trình: 7 + 4 3 x 2 + x - 1 = 2 + 3 x - 2 . Chọn khẳng định đúng trong các khẳng định sau:
A. Phương trình có hai nghiệm không dương.
B. Phương trình có hai nghiệm dương phân biệt.
C. Phương trình có hai nghiệm trái dấu.
D. Phương trình có hai nghiệm âm phân biệt.
Cho phương trình: 7 + 4 3 x 2 + x − 1 = 2 + 3 x − 2 Chọn khẳng định đúng trong các khẳng định sau:
A. Phương trình có hai nghiệm không dương.
B. Phương trình có hai nghiệm dương phân biệt.
C. Phương trình có hai nghiệm trái dấu.
D. Phương trình có hai nghiệm âm phân biệt.
Đáp án A
Phương pháp:
+) Biến đổi phương trình đã cho bằng công thức hằng đẳng thức của căn bậc hai và sử dụng các công thức lũy thừa.
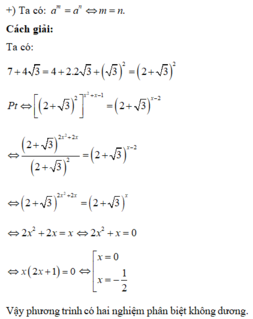
Cho phương trình sau 3 + 4 x = x - 2 . Chọn khẳng định đúng?
A. Phương trình có 1 nghiệm x < 2
B. Phương trình vô nghiệm.
C. Phương trình có vô số nghiệm.
D. Phương trình có hai nghiệm phân biệt
Điều kiện: x − 2 ≥ 0 ⇔ x ≥ 2
3 + 4 x = x - 2 ⇔ 3 + 4 x = x − 2 3 + 4 x = 2 − x ⇔ 3 x = − 5 5 x = − 1 ⇔ x = − 5 3 ( L ) x = − 1 5 ( L )
Vậy phương trình vô nghiệm
Đáp án cần chọn là: B
Chọn khẳng định đúng. Nếu phương trình a x 2 = m.x + n vô nghiệm thì đường thẳng d: y = mx + n và parabol (P): y = a x 2
A. Cắt nhau tại hai điểm
B. Tiếp xúc với nhau
C. Không cắt nhau
D. Cắt nhau tại gốc tọa độ
Đường thẳng d: y = mx + n và parabol (P): y = a x 2 không cắt nhau khi phương trình a x 2 = m . x + n vô nghiệm
Đáp án: C
Gọi x 0 là nghiệm của phương trình 3(x – 2) – 2x(x + 1) = 3 – 2 x 2 . Chọn khẳng định đúng.
A. x 0 là số nguyên âm
B. x 0 là số nguyên dương
C. x 0 không là số nguyên
D. x 0 là số vô tỉ
Gọi x 0 là nghiệm của phương trình 2.(x – 3) + 5x(x – 1) = 5 x 2 . Chọn khẳng định đúng.
A. x 0 > 0
B. x 0 < -2
C. x 0 > -2
D. x 0 > - 3
Cho hai phương trình 7(x – 1) = 13 + 7x (1) và x + 2 2 = x 2 + 2x + 2(x + 2) (2). Chọn khẳng định đúng
A. Phương trình (1) vô nghiệm, phương trình (2) có nghiệm duy nhất
B. Phương trình (1) vô số nghiệm, phương trình (2) có vô nghiệm
C. Phương trình (1) vô nghiệm, phương trình (2) có vô số nghiệm
D. Cả phương trình (1) và phương trình (2) đều có 1 nghiệm
Cho phương trình (1): x( x 2 – 4x + 5) = 0 và phương trình (2): ( x 2 – 1)( x 2 + 4x + 5) = 0.
Chọn khẳng định đúng
A. Phương trình (1) có một nghiệm, phương trình (2) có hai nghiệm
B. Phương trình (1) có hai nghiệm, phương trình (2) có một nghiệm
C. Hai phương trình đều có hai nghiệm
D. Hai phương trình đều vô nghiệm