Đáp án A
Phương pháp:
+) Biến đổi phương trình đã cho bằng công thức hằng đẳng thức của căn bậc hai và sử dụng các công thức lũy thừa.
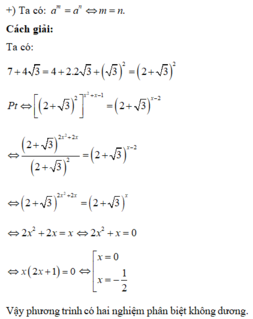
Đáp án A
Phương pháp:
+) Biến đổi phương trình đã cho bằng công thức hằng đẳng thức của căn bậc hai và sử dụng các công thức lũy thừa.
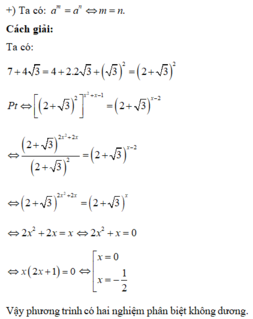
Xét các số nguyên dương a,b sao cho phương trình b ln 2 x + a ln x + 3 = 0 có hai nghiệm phân biệt x 1 , x 2 và phương trình 3 log 2 x + a log x + b = 0 có hai nghiệm phân biệt x 3 , x 4 thỏa mãn ln x 1 x 2 10 > log x 3 x 4 6 Tính giá trị nhỏ nhất của S=5a + 3b
A. 102
B. 101
C. 96
D. 99
Phương trình: z + 3 − i 2 − 6 z + 3 − i + 13 = 0 có 2 nghiệm phân biệt. Khẳng định nào sau đây là đúng?
A. Trong 2 nghiệm có một nghiệm bằng 0
B. Cả 2 nghiệm đều là số thực
C. Cả 2 nghiệm đều là số thuần ảo
D. Trong 2 nghiệm có 1 nghiệm là số thực, 1 nghiệm là số thuần ảo
Cho phương trình m ln 2 x + 1 - x + 2 - m ln x + 1 - x - 2 = 0 1 . Tập tất cả giá trị của tham số m để phương trình 1 có các nghiệm, trong đó có hai nghiệm phân biệt thỏa mãn 0 < x 1 < 2 < 4 < x 2 là khoảng a ; + ∞ . Khi đó, a thuộc khoảng
A. (3,8;3,9)
B. (3,7;3,8)
C. (3,6;3,7)
D. (3,5;3,6)
Cho hàm số f x liên tục trên đoạn a ; b và có đạo hàm trên khoảng a ; b
Cho các khẳng định sau:
i) Tồn tại một số c ∈ a ; b sao cho f ' c = f b − f a b − a .
ii) Nếu f a = f b thì luôn tồn tại c ∈ a ; b sao cho f ' c = 0.
iii) Nếu f x có hai nghiệm phân biệt thuộc khoảng a ; b thì giữa hai nghiệm đó luôn tồn tại một nghiệm của phương trình f ' x = 0.
Số khẳng định đúng trong ba khẳng định trên là
A. 0
B. 2
C. 3
D. 1
Cho phương trình y = x 3 - 6 x 2 + 9 x - 2 và các phát biểu sau:
(1) x = 0 là nghiệm duy nhất của phương trình
(2) Phương trình có nghiệm dương
(3) Cả 2 nghiệm của phương trình đều nhỏ hơn 1
(4) Phương trình trên có tổng 2 nghiệm là: - log 5 3 7
Số phát biểu đúng là:
A. 1
B. 2
C. 3
D. 4
Cho hàm số y = f(x) có đồ thị như hình vẽ dưới đây:
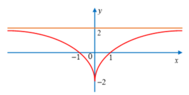
Trong các khẳng định sau:
I. Đồ thị hàm số có tiệm cận ngang là đường thẳng y = 2
II. Hàm số đạt cực tiểu tại x = -2
III. Hàm số nghịch biến trong khoảng − ∞ ; 0 và đồng biến trong khoảng 0 ; ∞
IV. Phương trình f(x) = m có hai nghiệm phân biệt khi và chỉ khi . Có bao nhiêu khẳng định đúng
A. 1
B. 2
C. 3
D. 4
Biết phương trình x3 – 3x + m = 0 có ba nghiệm phân biệt. Khẳng định nào sau đây đúng?
A. m2 ≤ 4
B. m2 ≥ 4
C. m2 > 4
D. m2 < 4
Cho phương trình (ẩn x) x2 – 2(m – 1)x + m2 = 0.
a) Tính ∆'.
b) Với giá trị nào của m thì phương trình có hai nghiệm phân biệt ? Có nghiệm kép ? Vô nghiệm ?
Giá trị của m làm cho phương trình ( m - 2 ) x 2 - 2 m x + m + 3 = 0 có hai nghiệm dương phân biệt là
A. m > 6
B. m < 6 và m≠2
C. 2 < m < 6 hoặc m < -3
D. m < 0 hoặc 2 < m < 6
Phương trình 3 . 9 x + 1 = 4 . 3 x có hai nghiệm a, b trong đó a < b. Khẳng định nào sau đây là đúng?
A.a + b = -2
B. a + 2b = -1
C. ab = -1
D. 2a + b = 0