Cho parabol (P): y = x 2 và d: y = 4x + 5. Tìm tọa độ giao điểm A, B của (P) và d:
A. A (−1; −1); B (5; 25)
B. A (−1; 1); B (−5; 25)
C. A (1; 1); B (5; 25)
D. A (−1; −1); B (−5; −25)
Những câu hỏi liên quan
trên cùng một MFTĐ Oxy cho hai đồ thị Parabol (P):y=x² và (d):y=-4x-3 a) vẽ (P) b) tìm tọa độ giao điểm của (P) và (d)
trên mặt phẳng tọa độ Oxy cho đường thẳng (d):y=-x+2 và Parabol (P):y=x² a)vẽ đồ thị của (d) và (P) trên cùng 1 hệ trục tọa độ b)Tìm tọa độ giao điểm của (P) và (d) (bằng phép tính) c) gọi A và B là 2 giao điểm của (d ) và (P). Tính diện tích tam giác OAB
a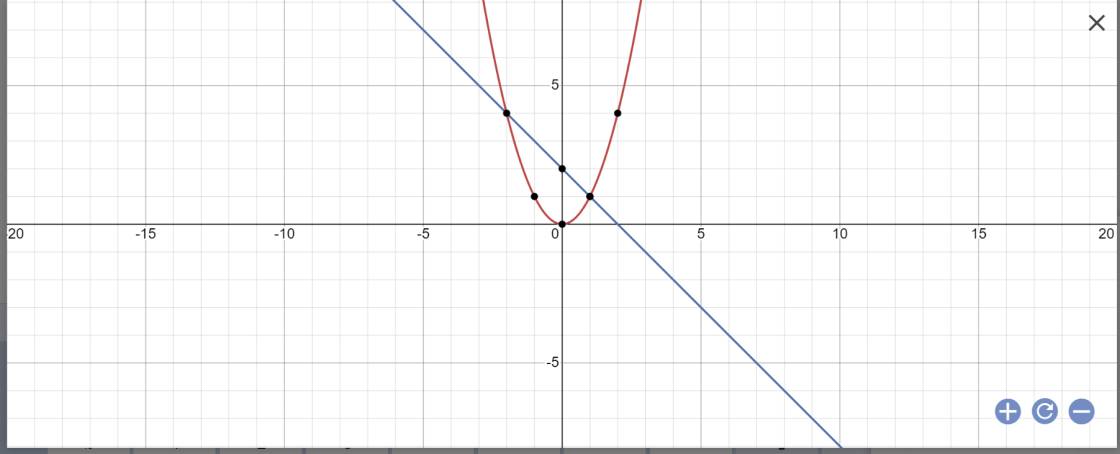
b:
PTHĐGĐ là:
x^2+x-2=0
=>(x+2)(x-1)=0
=>x=-2 hoặc x=1
=>y=4 hoặc y=1
Đúng 0
Bình luận (0)
cho parabol (p) : y=\(-\dfrac{x^2}{2}\)và đường thẳng y=\(-\dfrac{1}{2}x-1\) (d) trên cùng mặt tọa độ .a) vẽ parabol (P) và đường thẳng (d) trên cùng hệ trục tọa độ Oxy
b)tìm tọa độ giao điểm của (p) và (d) bằng phép tính
b: Phương trình hoành độ giao điểm là:
\(-\dfrac{1}{2}x^2=-\dfrac{1}{2}x-1\)
\(\Leftrightarrow-\dfrac{1}{2}x^2+\dfrac{1}{2}x+1=0\)
\(\Leftrightarrow x^2-x-2=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
Thay x=2 vào (P), ta được:
\(y=\dfrac{-2^2}{2}=-2\)
Thay x=-1 vào (P), ta được:
\(y=-\dfrac{1^2}{2}=-\dfrac{1}{2}\)
Đúng 2
Bình luận (0)
a ) Tìm tọa độ giao điểm của đường thẳng d : y = - x + 2 và Parabol : y = x2
b ) Cho hệ phương trình : \(\left\{{}\begin{matrix}4x+ay=b\\x-by=a\end{matrix}\right.\) . Tìm a và b để hệ đã cho có nghiệm duy nhất ( x , y ) = ( 2 : -1 )
a. Theo bài ra ta có: \(x^2+x-2=0\)
\(\left[{}\begin{matrix}x=-2\\x=1\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}y=-\left(-2\right)+2=4\\y=-1+2=1\end{matrix}\right.\)
Vậy tọa độ giao điểm cần tìm là: \(\left(-2;4\right)\); \(\left(1:1\right)\)
b. Thay x = 2 ; y = -1 vào hpt ta có:
\(\left\{{}\begin{matrix}8-a=b\\2+b=a\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}-a-b=-8\\-a+b=-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=5\\b=3\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho parabol (P) : y = x^2 và đường thẳng (d) : y = -x + 2
a, Tìm tọa độ giao điểm của (P) và (d)
b, Gọi A,B là 2 giao điểm của (P) và (d). Tính diện tích tam giác OAB
Bài 1. Trong mặt phẳng tọa độ Oxy, cho parabol (P): y - x2a) Vẽ parabol (P)b) Xác định tọa độ các giao điểm A, B của đường thẳng (d): y - x – 2 và (P).c) Tìm tọa độ điểm M trên (P) sao cho tam giác MAB cân tại MBài 2 Cho parabol (P): y x2 và đường thẳng (d): y x + mCMR: (d) luôn cắt (P) tại 2 điểm phân biệta) Giả sử (P) và (d) cắt nhau tại 2 điểm phân biệt có hoành độ x1; x2. Hãy tìm giá trị nhỏ nhất của biểu thức P khi m thay đổiBài 3. Cho parabol (P): y x2 và đường...
Đọc tiếp
Bài 1. Trong mặt phẳng tọa độ Oxy, cho parabol (P): y = - x2
a) Vẽ parabol (P)
b) Xác định tọa độ các giao điểm A, B của đường thẳng (d): y = - x – 2 và (P).
c) Tìm tọa độ điểm M trên (P) sao cho tam giác MAB cân tại M
Bài 2 Cho parabol (P): y = x2 và đường thẳng (d): y = x + m
CMR: (d) luôn cắt (P) tại 2 điểm phân biệt
a) Giả sử (P) và (d) cắt nhau tại 2 điểm phân biệt có hoành độ x1; x2. Hãy tìm giá trị nhỏ nhất của biểu thức P = 
khi m thay đổi
Bài 3. Cho parabol (P): y = x2 và đường thẳng (d): y = x + m
Tìm m để đường thẳng (d) cắt (P) tại 2 điểm phân biệt nằm bên phải trục tung
Bài 4. Cho parabol (P): y = x2 và đường thẳng (d): y = x + m
Bài 5. Cho parabol (P): y = x2 và đường thẳng (d): y = mx + 1
Tìm m sao cho (d) cắt (P) tại 2 điểm phân biệt có hoành độ x1; x2 sao cho 
Bài 6. Cho parabol (P) : y = 
x2 và đường thẳng (d) : y = mx - m2 + m +1.
a) Với m = 1, xác định tọa độ các giao điểm A, B của (d) và (P).
b) Tìm các giá trị của m để (d) cắt (P) tại hai điểm phân biệt có hoành độ x1, x2 sao cho 
.
30 tháng 5 2023 lúc 9:00
Trong mặt phẳng tọa độ Oxy cho parabol y=-x² và đường thẳng (d)y=-4x+3 a.Vẽ P và d b.Tìm tọa độ giao điểm A,B của P và d.Tính độ dài đoạn thẳng AB c.Tìm điểm thuộc P(khác góc tọa độ O có hoành độ dương và cách đều 2 trục tọa độ)
a: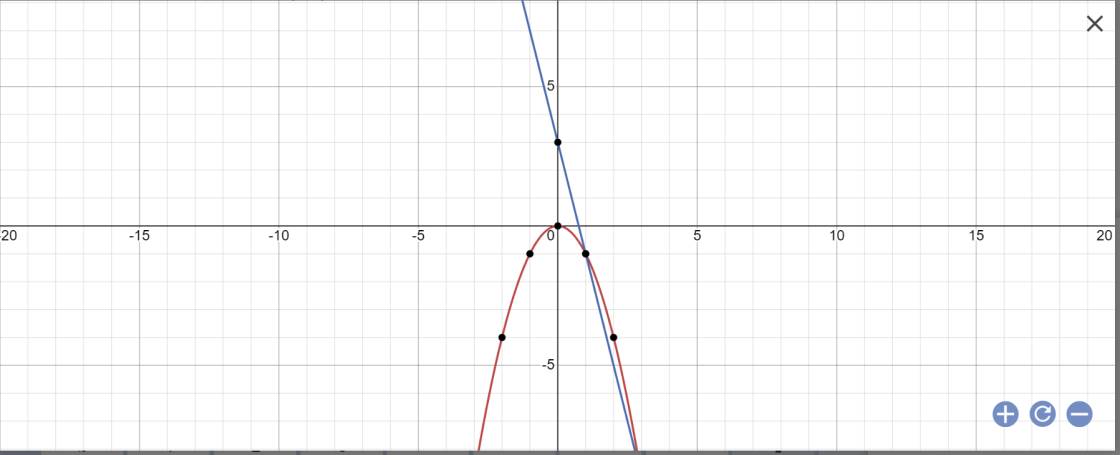 
b: PTHĐGĐ là:
-x^2+4x-3=0
=>x^2-4x+3=0
=>x=1;x=3
=>A(1;-1); B(3;-9)
c: \(AB=\sqrt{\left(3-1\right)^2+\left(-9+1\right)^2}=2\sqrt{17}\)
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho Parabol (P): y=x^2 và đường thẳng (d): y=-x+2
a, Vẽ đồ thị của 2 hàm số trên cùng 1 hệ trục tọa độ
b, Tìm tọa độ giao điểm của (P) và (d)
c, Gọi A,B là 2 giao điểm của (P) và (d). Tính diện tích tam giác OAB
a: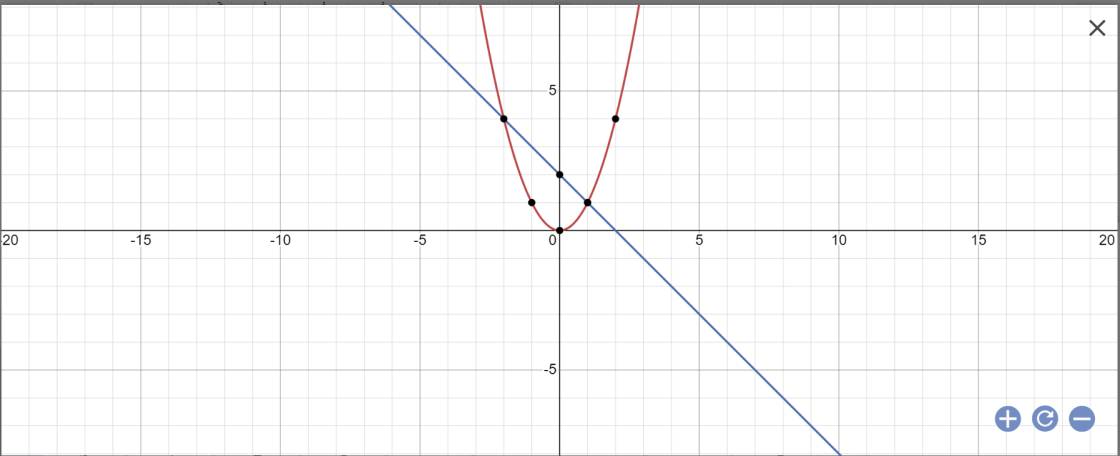 
b: PTHĐGĐ là:
x^2+x-2=0
=>(x+2)(x-1)=0
=>x=-2 hoặc x=1
=>y=4 hoặc y=1
Đúng 0
Bình luận (0)
Cho parabol (P): y = x2 và đường thẳng (d): y = -1/2 x + 3.
a) Tìm tọa độ các giao điểm A và B của (d) và (P).
b) Tìm tọa độ điểm C thuộc trục hoành để chu vi tam giác ABC đạt già trị lớn nhất.