Cho tam giác ABC, góc A bằng 90 độ, đường cao AH. Gọi E,F lần lượt là hình chiếu của H trên AB, AC.
a) Tứ giác EAFH là hình gì?
b) Qua A kẻ đường vuông góc với EF cắt BC tại I. Chứng minh: I là trung điểm của BC
Giúp em câu b với ạ
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A đường cao AH . gọi E,F lần lượt là chân đường vuông góc . kẻ từ H đến AB,AC a/ Tứ giác EAFH là hình gì? b/ Qua A kẻ đường vuông góc với EF cắt BC ở I . chứng minh I là trung điểm BC.
a: Xét tứ giác EAFH có
\(\widehat{EAF}=\widehat{AEH}=\widehat{AFH}=90^0\)
Do đó: EAFH là hình chữ nhật
Đúng 0
Bình luận (0)
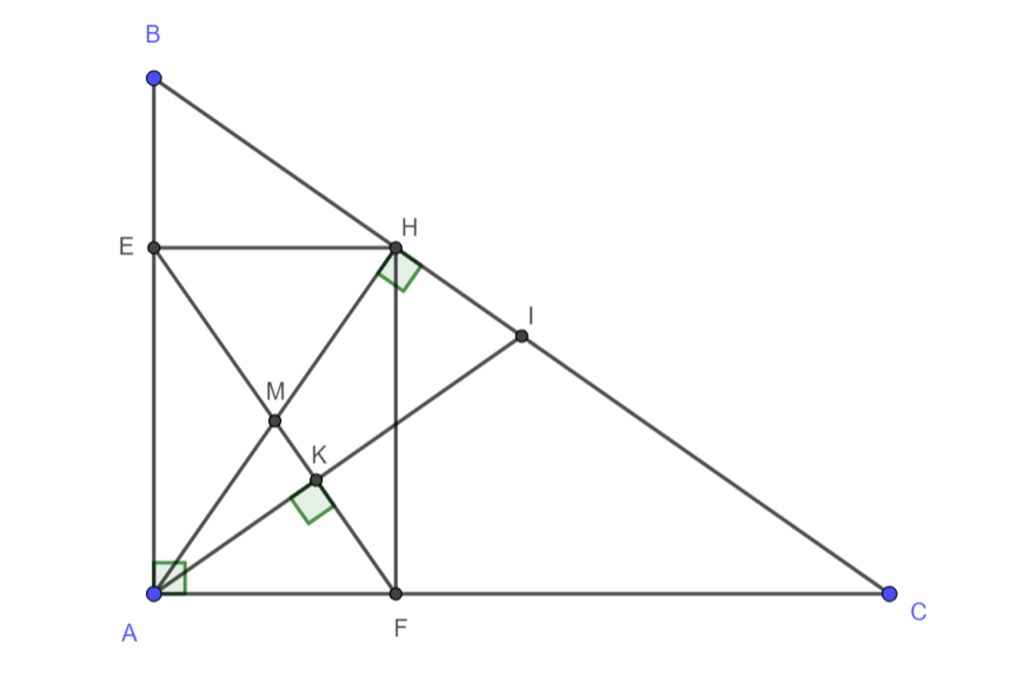
a) Xét tứ giác AEHF có:
∠A = ∠E = ∠F= 90o
⇒ AEHF là hình chữ nhật (dấu hiệu nhận biết)
b) Gọi M = AH∩EF
K = AI∩EF
Vì ∠K = ∠H = 90o
∠A chung
⇒ ΔAKM và ΔAHI đồng dạng (g.g)
⇒ ∠AMK = ∠AIH (hai góc tương ứng)
Vì tứ giác AEHF là hình chữ nhật (cmt)
⇒ Giao điểm của hai đường chéo là trung điểm của mỗi đường và hai đường chéo bằng nhau
⇒
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A đường cao AH . gọi E,F lần lượt là chân đường vuông góc . kẻ từ H đến AB,AC
a/ Tứ giác EAFH là hình gì?
b/ Qua A kẻ đường vuông góc với EF cắt BC ở I . chứng minh I là trung điểm BC. Giúp mik vs 😥
a) Xét tứ giác EAFH có
\(\widehat{AFH}=90^0\)
\(\widehat{FAE}=90^0\)
\(\widehat{AEH}=90^0\)
Do đó: EAFH là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
b) Ta có: \(\widehat{IAC}=90^0-\widehat{AFE}\)
\(\widehat{ICA}=90^0-\widehat{B}\)
mà \(\widehat{AFE}=\widehat{B}\left(=\widehat{HAC}\right)\)
nên \(\widehat{IAC}=\widehat{ICA}\)
mà \(\widehat{IBA}=90^0-\widehat{ICA}\)
và \(\widehat{IAB}=90^0-\widehat{IAC}\)
nên \(\widehat{IAB}=\widehat{IBA}\)
Xét ΔIAB có \(\widehat{IAB}=\widehat{IBA}\)(cmt)
nên ΔIAB cân tại I(Định lí đảo của tam giác cân)
Xét ΔIAC có \(\widehat{IAC}=\widehat{ICA}\)(cmt)
nên ΔIAC cân tại I(Định lí đảo của tam giác cân)
Ta có: IA=IB(ΔIAB cân tại I)
IA=IC(ΔIAC cân tại I)
Do đó: IB=IC
mà I nằm giữa B và C
nên I là trung điểm của BC(Đpcm)
Đúng 3
Bình luận (1)
Cho tam giác ABC vuông ở A , đường cao AH . Gọi E và F lần lượt là chân đường vuông góc kẻ từ H đến AB , AC
a ) Tứ giác EAFH là hình gì ?
b ) Qua A kẻ đường thẳng vuông góc với EF cắt BC ở I . Chứng minh I là trung điểm ở BC
Cho tam giác ABC vuông tại A, Đường cao AH , Gọi E và F lần lượt là chân đường vuông góc kẻ từ H đến AB và AC
a, Tứ giác EAFH là hình gì?
b, Qua A kẻ đường vuông góc với EF cắt BC ở I. CM: I là trung điểm của BC
a, xét tứ giác AEHF có :
góc BAC = 90 do tam giác ABC vuông tại A (gt)
góc HEA = 90 do HE _|_ AB (Gt)
góc HFA = 90 do HF _|_ AC (gt)
=> tứ giác AEHF là hình chữ nhật (dh)
Cho tam giác ABC vuông tại A đường cao AH. Gọi E,F lần lượt là chân đường vuông góc kẻ đến AB, AC
a, cm tứ giác EAFH là hình gì
b, qua A kẻ đường thẳng vuông góc với EF cắt BC ở I. cm I là trung điểm BC
cho tam giác abc vuông tại a,đường cao ah. gọi e,f lần lượt là chân đường vuông góc kẻ từ h đến ab,ac
a:tứ giác eafh là hình gì ?
b:qua a kẻ đường vuông góc với ef,cắt bc tại i. chứng minh i là trung điểm của bc
Tam giác ABC vuông tại A , đường cao AH , E và F lần lượt là các chân đường vuông góc kẻ từ H đến AB và AC
a, Tứ giác EAFH là hình gì ?
b, Qua A kẻ vuông góc với ÈF cắt BC ở I . Chứng minh I là trung điểm của BC
Cho tam giác ABC vuông tại A, AH là đường cao (H thuộc BC). Kẻ HE, HF lần lượt vuông góc với AB và AC (E thuộc AB, F thuộc AC). a)Chứng minh AH=EF.
b)Gọi O là giao điểm của AH và EF, K là trung điểm của AC. Qua F kẻ đường thẳng vuông góc với EF cắt BC ở I. Chứng minh tứ giác AOIK là hình bình hành
Cho tam giác ABC vuông tại A, có BC a không đổi. Kẻ đường cao AH. Gọi E, F lần lượt là hình chiếu của H trên các cạnh AB và AC
a) Chứng minh tứ giác AEHF là hình chữ nhật
b) Gọi M là trung điểm của BH Chứng minh góc MEF bằng 90 độ
c) Gọi N là trung điểm của CH. Tứ giác MEFN là hình gì hãy chứng minh
d) Tìm điều kiện của tam giác vuông ABC để EF có độ dài lớn nhất
Đọc tiếp
Cho tam giác ABC vuông tại A, có BC = a không đổi. Kẻ đường cao AH. Gọi E, F lần lượt là hình chiếu của H trên các cạnh AB và AC
a) Chứng minh tứ giác AEHF là hình chữ nhật
b) Gọi M là trung điểm của BH Chứng minh góc MEF bằng 90 độ
c) Gọi N là trung điểm của CH. Tứ giác MEFN là hình gì hãy chứng minh
d) Tìm điều kiện của tam giác vuông ABC để EF có độ dài lớn nhất
cho tam giác ABC vuông tại A đường cao AH gọi E và F lần lượt là chân đường vuông góc kẻ từ H đến AB và AC. Chứng minh
a) định dạng tứ giác EAFH
b) qua A kẻ đường thẳng vuông góc với E cắt BC tạo I. chứng minh IB = IC