Bài 1: Cho hình bình hành ABCD có AB: x-y+2=0 và BC: 2x-y+3=0. Tâm hình bình hành là I(3;8).
a, Tìm toạ độ đỉnh A,C
b, Viết phương trình các cạnh còn lại của hình bình hành
c, Tìm tọa độ các đỉnh còn lại
giúp em với ạ!!
Những câu hỏi liên quan
cho hình bình hành ABCD biết AB 2x - y = 0 AD 4x - 3y =0 và tâm I ( 2,2) lập pt các cạnh BC và CD
Trong (Oxy), cho hình bình hành ABCD có tâm I(1;2) và hai đường thẳng AB, AD lần lượt có phương trình là x + 3y - 6 = 0 và 2x - 5y - 1 = 0. Viết phương trình đường thẳng BC và CD.
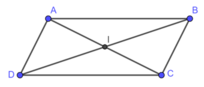
Ta có: A là giao điểm của AB và AD. Do đó, tọa độ A là nghiệm của hệ phương trình:
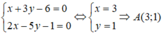
Hình bình hành ABCD có tâm I nên I là trung điểm của AC và BD ⇒ C(-1;3)
Đường thẳng BC đi qua C và song song với AD
Vì BC song song với AD nên BC có dạng: 2x - 5y + c = 0, (c ≠ -1)
Vì C thuộc BC nên: 2.(-1) - 5.3 + c = 0 ⇒ c = 17(tm)
Vậy phương trình đường thẳng BC là: 2x - 5y + 17 = 0
Đường thẳng DC đi qua C và song song với AB
Vì DC song song với AB nên DC có dạng: x + 3y + c = 0, (c ≠ -6)
Vì C thuộc DC nên: -1 + 3.3 + c = 0 ⇒ c = -8(tm)
Vậy phương trình đường thẳng DC là: x + 3y - 8 = 0
Đúng 0
Bình luận (1)
Cho hình bình hành ABCD ncos phương trình đường chéo AC: x-y+1=0 điểm G(1;4) là trọng tâm tam giác ABC điểm E(0;-3) thuộc đường cao kẻ từ D của tam giác ACD. Tìm toạ độ các đỉnh của hình bình hành cho S tứ giác AGCD=32 và tung độ yA>0
http://tin.tuyensinh247.com/de-thi-thu-dai-hoc-mon-toan-khoi-b-nam-2014-lan-cuoi-thpt-chuyen-dh-vinh-c31a17586.html
Cau 7a nha
Đúng 0
Bình luận (0)
câu1:
a, 4x . ( 3x^2 - 4xy + 6y^2 )
b, 2x/3x -3y . x^3/x-y
c,( 6x^4y^3 - 15x^3y^2 + 9x^2y^2 ) : 3xy
câu2:
cho hình bình hành ABCD , gọi EFGH lần lượt là trung điểm của các cạnh AB,BC,CD,DA
a, Chứng minh tứ giác EFGH là hình bình hành
b, khi Hình bình hành ABCD là hình chữ nhật thì tứ giác ABCD là hình gì ? vì sao
câu 10 cho hình bình hành ABCD (AB//GÓC D=130\(^0\)
CD và góc B - góc C =50\(^0\)hãy tính các góc còn lại của hình thang
câu 11 cho hình bình hành ABCD có góc A =3 lần góc B.Hãy tính số đo góc của hình bình hành
Câu 10:
góc A=180-130=50 độ
góc B=(180+50)/2=230/2=115 độ
góc C=180-115=65 độ
Đúng 1
Bình luận (0)
Câu 1:cho hình bình hành ABCD tâm O chứng minh BD-BA=OC-OB và BC-BD+BA=O
Câu 2: cho hình bình hành ABCD tâm O. m là điểm tuỳ ý chứng minh AB+OA=OB và MA+MC=MB+MD
Xem chi tiết
Câu 1: giả sử:\(\overrightarrow{BD}-\overrightarrow{BA}=\overrightarrow{OC}-\overrightarrow{OB}\Leftrightarrow\overrightarrow{BA}+\overrightarrow{AD}-\overrightarrow{BA}=\overrightarrow{OC}+\overrightarrow{BO}\)
\(\Leftrightarrow\overrightarrow{AD}=\overrightarrow{BC}\)(luôn đúng vì ABCD lad hình bình hành)
giả sử: \(\overrightarrow{BC}-\overrightarrow{BD}+\overrightarrow{BA}=\overrightarrow{0}\Leftrightarrow\overrightarrow{BC}-\overrightarrow{BC}+\overrightarrow{DC}+\overrightarrow{BA}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{BB}+\overrightarrow{DD}=\overrightarrow{0}\)(LUÔN ĐÚNG)
câu 2 :GIẢ SỬ:
\(\overrightarrow{AB}+\overrightarrow{OA}=\overrightarrow{OB}\Leftrightarrow\overrightarrow{AO}+\overrightarrow{OB}+\overrightarrow{OA}+\overrightarrow{BO}=\overrightarrow{0}\)(luôn đúng)
giả sử: \(\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{MB}+\overrightarrow{MD}\\ \Leftrightarrow\overrightarrow{MB}+\overrightarrow{BA}+\overrightarrow{MD}+\overrightarrow{DC}=\overrightarrow{MB}+\overrightarrow{MD}\Leftrightarrow\overrightarrow{0}=\overrightarrow{0}\)
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD có tâm I, đường thẳng qua B vuông góc với BD cắt AI tại M, đường thẳng qua D vuông góc với BD cắt AB tại N. Biết pt DM: x+y-4=0, điểm E(5;0) thuộc NI, trung điểm của BI là P(-1/2;-3). Tìm tọa độ A,B,C,D
Bài 22: Cho hình bình hành ABCD có M và N là trung điểm của AB và CD. Chưng minh:1) Tư giác AMND là hình bình hành.2) Tư giác BMDN là hình bình hành.Bài 24: Cho hình bình hành ABCD có AB AD. Tia phân giác của widehat{A}căt BC tại I, tia phân giác của widehat{C}căt AD ở K.1) Chưng minh: Tam giác ABI là tam giác cân.2) So sánh widehat{BIA}và widehat{KCB}.3) Chưng minh: Tư giác AICK là hình bình hành.
Đọc tiếp
Bài 22: Cho hình bình hành ABCD có M và N là trung điểm của AB và CD. Chưng minh:
1) Tư giác AMND là hình bình hành.
2) Tư giác BMDN là hình bình hành.
Bài 24: Cho hình bình hành ABCD có AB < AD. Tia phân giác của \(\widehat{A}\)căt BC tại I, tia phân giác của \(\widehat{C}\)căt AD ở K.
1) Chưng minh: Tam giác ABI là tam giác cân.
2) So sánh \(\widehat{BIA}\)và \(\widehat{KCB}\).
3) Chưng minh: Tư giác AICK là hình bình hành.
Bài 22 :
Vì ABCD là hình bình hành
=> AB = DC
Mà M là trung điểm AB
=> AM = MB
Mà N là trung điểm DC
=> DN = NC
=> AM = DN
Mà AB//DC
=> DN//AM
=> AMND là hình bình hành
Chứng minh tương tự ta có : MBCN là hình bình hành
Đúng 0
Bình luận (0)
Kết quả của phép nhân: ( - 2x 2 y).3xy 3 bằng:A. 5x 3 y 4B. – 6x 3 y 4C. 6x 3 y 4D. 6x 2 y 3ABCDHình nào sau đây có 4 trục đối xứng ?A. Hình thang cânB. Hình bình hànhC. Hình chữ nhậtD. Hình vuôngABCDCho hình bình hành ABCD có số đo góc A 105 0 , vậy số đo góc D bằng:A. 70 0B. 75 0C. 80 0D. 85 0
Đọc tiếp
Kết quả của phép nhân: ( - 2x 2 y).3xy 3 bằng:A. 5x 3 y 4B. – 6x 3 y 4C. 6x 3 y 4D. 6x 2 y 3ABCDHình nào sau đây có 4 trục đối xứng ?A. Hình thang cânB. Hình bình hànhC. Hình chữ nhậtD. Hình vuôngABCDCho hình bình hành ABCD có số đo góc A = 105 0 , vậy số đo góc D bằng:A. 70 0B. 75 0C. 80 0D. 85 0
Trong mặt phẳng tọa độ Oxy cho A(3; -1) ; B( -1; 2) và I( 1; -1) . Xác định tọa độ các điểm C; D sao cho tứ giác ABCD là hình bình hành biết I là trọng tâm tam giác ABC. Tìm tọa tâm O của hình bình hành ABCD A. B. C. D.
Đọc tiếp
Trong mặt phẳng tọa độ Oxy cho A(3; -1) ; B( -1; 2) và I( 1; -1) . Xác định tọa độ các điểm C; D sao cho tứ giác ABCD là hình bình hành biết I là trọng tâm tam giác ABC. Tìm tọa tâm O của hình bình hành ABCD
A. 
B. 
C. 
D. 
