Cho tam giác ABC vuông tại A.
1. Kẻ BD là tia phân giác của góc ABC ( D thuộc AC ), DH vuông góc với BC ( H thuốc BC ). Chứng minh DA = DH.
2. Trên tia đối của tia AB lấy M sao cho AM=CH. Chứng minh D,M,H thẳng hàng.
Cho tam giác ABC vuông tại A.
1. Kẻ BD là tia phân giác của góc ABC ( D thuộc AC ), DH vuông góc với BC ( H thuốc BC ). Chứng minh DA = DH.
2. Trên tia đối của tia AB lấy M sao cho AM=CH. Chứng minh D,M,H thẳng hàng.
GT | △ABC (BAC = 90o). BAD = DAC = ABC/2 (D DH ⊥ BC (H |
KL | 1, DA = DH 2, D, M, H thẳng hàng |
Bài giải:
1, Xét △DAB vuông tại A và △DHB vuông tại H
Có: ABD = DBH (gt)
BD là cạnh chung
=> △DAB = △DHB (ch-gn)
=> DA = DH
2, Xét △MAD vuông tại A và △CHD vuông tại H
Có: AD = DH (cmt)
AM = CH (gt)
=> △MAD = △CHD (2cgv)
=> MDA = HDC (2 góc tương ứng)
Ta có: HDC + HDA = 180o (2 góc kề bù)
=> MDA + HDA = 180o
=> MDH = 180o
=> D, M, H thẳng hàng
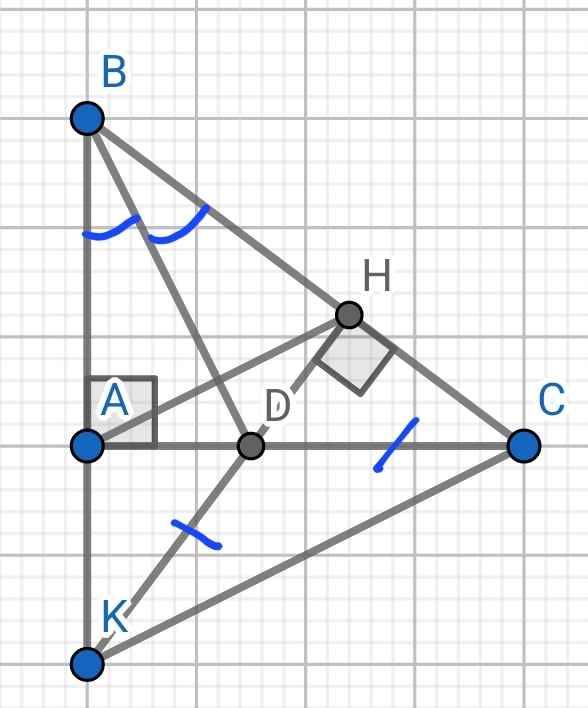
Cho tam giác ABC vuông tại A biết AB = 9 cm AC bằng 12 cm Kẻ BD là tia phân giác của góc B( d thuộc AC) kẻ dh vuông góc với BC( H thuộc BC). Trên tia đối của tia ab lấy điểm K sao cho a k = HC a) Chứng minh tam giác ABD= tam giác HBD b) So sánh DA và DC c) Chứng minh ba điểm k,d,hthẳng hàng
a: Xét ΔBAD vuông tại A và ΔBHD vuông tại H có
BD chung
góc ABD=góc HBD
=>ΔBAD=ΔBHD
b: ΔBAD=ΔBHD
=>DA=DH
mà DH<DC
nên DA<DC
c: Xét ΔDAK vuông tại A và ΔDHC vuông tại H có
DA=DH
AK=HC
=>ΔDAK=ΔDHC
=>góc ADK=góc HDC
=>góc HDC+góc KDC=180 độ
=>K,D,H thẳng hàng
cho tam giác ABC vuông tại A . Kẻ BD là tia phân giác ( D thuộc AC)
a) Biết AB = 4cm ; AC = 3cm . Tính BC
b)Qua D kẻ DH vuông góc BC( H thuộc BC ).Chứng minh BH = AH
c) Kẻ AM vuông góc BC tại M ( M thuộc BC) . Chứng minh AH là tia phân giác của góc MAC
D) Gọi K là giao điểm của AM = BD : C/m tam giác ADK cân
a: BC=5cm
b: Xét ΔBAD vuông tại A và ΔBHD vuông tại H có
BD chung
\(\widehat{ABD}=\widehat{HBD}\)
Do đó: ΔBAD=ΔBHD
Suy ra: BA=BH
c: \(\widehat{MAH}+\widehat{BHA}=90^0\)
\(\widehat{CAH}+\widehat{BAH}=90^0\)
mà \(\widehat{BHA}=\widehat{BAH}\)
nên \(\widehat{MAH}=\widehat{CAH}\)
hay AH là tia phân giác của góc MAC
mọi người giúp mình câu d với ạ ,mình sắp thi rùi ạ
cho tam giác ABC vuông tại A . Kẻ BD là tia phân giác ( D thuộc AC)
a) Biết AB = 4cm ; AC = 3cm . Tính BC
b)Qua D kẻ DH vuông góc BC( H thuộc BC ).Chứng minh BH = AH
c) Kẻ AM vuông góc BC tại M ( M thuộc BC) . Chứng minh AH là tia phân giác của góc MAC
D) Gọi K là giao điểm của AM = BD : C/m tam giác ADK cân
( mn giúp mình câu d vs ạ mình sắp thi rùi ạ )
Tham khảo
a: BC=5cm
b: Xét ΔBAD vuông tại A và ΔBHD vuông tại H có
BD chung
ˆABD=ˆHBD
Do đó: ΔBAD=ΔBHD
Suy ra: BA=BH
c: ˆMAH+ˆBHA=900
ˆCAH+ˆBAH=900
mà ˆBHA=ˆBAH
nên ˆMAH=ˆCAH
hay AH là tia phân giác của góc MAC
cho tam giác ABC vuông tại A.Từ B kẻ tia phân giác cắt AC tại D, kẻ DH vuông góc với BC(H thuộc BC).a) Chứng minh BD là đường trung trực của AH. b) Trên tia đối của tia AB lấy M sao cho BM=2xAC. Tính góc BMC với góc B = 750
Bài 4: (3 điểm) Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC (H thuộc BC). Kẻ HD, HE lần lượt vuông góc với AB và AC (D thuộc AB, E thuộc AC). Trên tia đối của tia DH lấy điểm M; trên tia đối của tia EH lấy điểm N sao cho DM = DH; EN = EH.
a) Chứng minh tam giác ABH = ACH ;
b) Chứng minh tam giác AMN là tam giác cân, từ đó suy ra góc BAC = 1/2 góc MAN
c) Chứng minh MN//DE.
d) Cho AB = 5cm, BC = 6cm. Tính độ dài BD.
Thấy cái ý △AMN cân với cái chứng minh BAC = 1/2 MAN cũng ko lên quan lắm. Tham khảo qua ạ tại câu b hơi có vấn đề :(
a) Xét △AHB và △AHC có:
AHB = AHC (= 90o)
AH: chung
AB = AC (△ABC cân)
=> △AHB = △AHC (ch-cgv)
b) Xét △ADM và △ADH có:
ADM = ADH (= 90o)
DM = DH (gt)
AD: chung
=> △ADM = △ADH (2cgv)
=> AM = AH (2 cạnh tương ứng) (1)
Xét △ANE và △AHE có:
AEH = AEN (= 90o)
EH = EN (gt)
AE: chung
=> △ANE = △AHE (2cgv)
=> AN = AH (hai cạnh tương ứng) (2)
Từ (1) và (2) => AM = AN => △AMN cân tại A
Ta có: MAN = MAB + BAH + HAC + CAN
Mà MAB = HAB, HAC = CAN (suy ra được từ các tam giác bằng nhau)
=> MAN = 2BAH + 2 HAC
=> MAN = 2BAC
=> BAC = 1/2MAN
c) Ta có: HAD = HAE (△AHB = △AHC)
Mà HAD = DAM, HAE = EAN
=> HAD + DAM = HAE + EAN
=> HAM = HAN
Gọi giao điểm AH và MN là F
Xét △AFM và △AFN có:
AF: chung
FAM = FAN (cmt)
AM = AN (cmt)
=> △AFM = △AFN (c.g.c)
=> AFM = AFN (2 góc tương ứng)
Mà AFM + AFN = 180o => AFM = AFN = 90o
=> AH vuông góc MN (1)
Gọi giao điểm của DE và AH là I
Xét △ADH và △AEH có:
ADH = AEH (= 90o)
AH: chung
HAD = HAE (△HAB = △HAC)
=> △ADH = △AEH (ch-gn)
=> AD = AE (2 cạnh tương ứng)
Xét △AID và △AIE có:
AI: chung
IAD = IAE (cmt)
AD = AE (cmt)
=> △AID = △AIE (c.g.c)
=> AID = AIE (2 góc tương ứng)
Mà AID + AIE = 180o => AID = AIE = 90o
=> AH vuông góc DE (2)
Từ (1) và (2) => MN // DE
d) \(\Delta\)ABC cân tại A có AH là đường cao
=> AH là đường trung tuyến
=> H là trung điểm BC
=> BH = HC = BC : 2 = 3 ( cm )
\(\Delta\)ABH vuông tại H => AB2 - BH2 = AH2 => AH = 4 cm
=> S ( \(\Delta\)ABH ) = \(\frac{1}{2}\)BH . AH =\(\frac{1}{2}\) HD . AB
=> 3.4 = HD . 5 => HD = 2,4 cm
\(\Delta\)BDH vuông tại D => BD2 = BH2 - HD2 = 3,24 => BD = 1,8 cm
Cho tam giác ABC vuông tại A. Tia phân giác của góc B cắt AC tại D. Kẻ DH vuông góc với BC tại H. Trên tia đối của tia DH lấy điểm K sao cho DK = DC
a) Chứng minh \(\Delta\)ABD = \(\Delta\)HBD
b) Chứng minh BD là đường trung trực của AH
c) Chứng minh ba điểm B,A,K thẳng hàng
a) Xét hai tam giác vuông: ∆ABD và ∆HBD có:
BD chung
∠ABD = ∠HBD (BD là phân giác của ∠ABH)
⇒ ∆ABD = ∆HBD (cạnh huyền - góc nhọn)
b) Do ∆ABD = ∆HBD (cmt)
⇒ AB = BH (hai cạnh tương ứng)
⇒ B nằm trên đường trung trực của AH (1)
Do ∆ABD = ∆HBD (cmt)
⇒ AD = HD (hai cạnh tương ứng)
⇒ D nằm trên đường trung trực của AH (2)
Từ (1) và (2) ⇒ BD là đường trung trực của AH
c) Xét ∆ADK và ∆HDC có:
AD = HD (cmt)
∠ADK = ∠HDC (đối đỉnh)
DK = DC (gt)
⇒ ∆ADK = ∆HDC (c-g-c)
⇒ ∠DAK = ∠DHC (hai góc tương ứng)
⇒ ∠DAK = 90⁰
Mà ∠DAB = 90⁰
⇒ ∠DAK + ∠DAB = 180⁰
⇒ B, A, K thẳng hàng
Cho tam giác ABC có AB=AC và M là trung điểm của BC. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD=CE
a) Chứng minh tam giác ABM= tam giác ACM từ đó suy ra AM vuông góc vs BC
b) Chứng minh tam giác ABD= tam giác ACE từ đó suy ra AM là tia phân giác của góc DAE
c) Kẻ BK vuông góc AD( K thuộc AD) trên tia đối của tia BK lấy điểm H sao cho BH=AE, trên tia đối của tia AM lấy điểm N sao cho AN=CE, Chứng minh góc MAD= góc MBH
d) Chứng minh Dn vuông góc DH
Cho tam giác ABC có AB=AC và M là trung điểm của BC. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD=CE
a) Chứng minh tam giác ABM= tam giác ACM từ đó suy ra AM vuông góc vs BC
b) Chứng minh tam giác ABD= tam giác ACE từ đó suy ra AM là tia phân giác của góc DAE
c) Kẻ BK vuông góc AD( K thuộc AD) trên tia đối của tia BK lấy điểm H sao cho BH=AE, trên tia đối của tia AM lấy điểm N sao cho AN=CE, Chứng minh góc MAD= góc MBH
d) Chứng minh Dn vuông góc DH
Hình bạn tự vẽ nhé ![]()
a) Xét ΔABM và ΔACM có:
AB=AC (gt)
AM là cạnh chung
BM=CN (M là trung điểm của BC)
=> ΔABM=ΔACM (c-c-c)
=> \(\widehat{AMB}=\widehat{AMC}\) (2 góc tương ứng)
Mà ta có: \(\widehat{AMB}+\widehat{AMC}=90^o\)
=> \(\widehat{AMB}+\widehat{AMB}=180^o\)
=> \(\widehat{AMB}=90^o\)
=> AM vuông góc với BC
b) Theo câu a ta có: ΔABM=ΔACMB
=> \(\widehat{ABM}=\widehat{ACM}\)
Mà: \(\widehat{ABD}=180^o-\widehat{ABM}=180^o-\widehat{ACM}=\widehat{ACE}\)
Xét ΔABD và ΔACE có:
AB=AC (gt)
\(\widehat{ABD}=\widehat{ACE}\) (chứng minh trên)
BD=CE (gt)
=> ΔABD=ΔACE (c-g-c)
=> \(\widehat{BAD}=\widehat{CAE}\) (2 góc tương ứng)
Cũng theo câu a thì ΔABM=ΔACM
=> \(\widehat{BAM}=\widehat{CAM}\)
=> \(\widehat{BAM}+\widehat{BAD}=\widehat{CAM}+\widehat{CAE}\)
=> \(\widehat{DAM}=\widehat{EAM}\)
=> AM là tia phân giác của góc DAE
Cho tam giác ABC có AB=AC và M là trung điểm của BC. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD=CE
a) Chứng minh tam giác ABM= tam giác ACM từ đó suy ra AM vuông góc vs BC
b) Chứng minh tam giác ABD= tam giác ACE từ đó suy ra AM là tia phân giác của góc DAE
c) Kẻ BK vuông góc AD( K thuộc AD) trên tia đối của tia BK lấy điểm H sao cho BH=AE, trên tia đối của tia AM lấy điểm N sao cho AN=CE, Chứng minh góc MAD= góc MBH
d) Chứng minh Dn vuông góc DH
a, xét tam giác AMB và tam giác AMC có : AM chung
BM = CM do M là trung điểm của BC (gt)
AB = AC (gt)
=> tam giác AMB = tam giác AMC (c-c-c)
=> góc AMB = góc AMC (đn)
mà góc AMB + góc AMC = 180 (kb)
=> góc AMB = 90
=> AM _|_ BC (đn)
b, góc ABC = góc ACB do tam giác ABC cân tại A (gt)
góc ABC + góc ABD = 180 (kb)
góc ACB + góc ACE = 180 (kb)
=> góc ABD = góc ACE
xét tam giác ABD và tam giác ACE có : BD = CE (gt)
AB = AC (gt)
=> tam giác ABD = tam giác ACE (c-g-c)