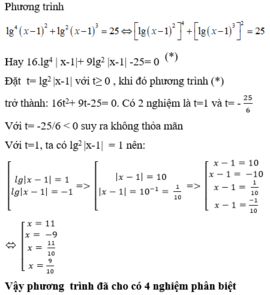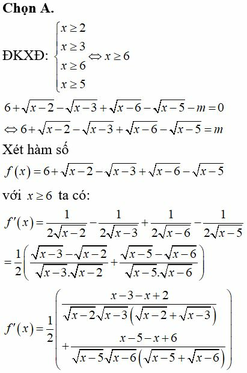Giải phương trình \(2^{2^x}+3^{2^x}=2^x+3^{x+1}+x+1\) có bao nhiêu nghiệm thực
Những câu hỏi liên quan
Bài 1: Phương trìnhlog_{2} ^3(x-1)-27y^3+8^y+1-x có bao nhiêu (x;y) nghiệm thuộc [8^{1992}; 8^{2020}]Bài 2: Tìm tập hợp số thực m để phương trình 2^{2x-1}+m×2^x+2m-20 có 2 nghiệm thực phân biệt thuộc đoạn [1;2]Bài 3: Tìm các số nguyên m để phương trình log_{dfrac{1}{2}}^{2} (x-2)^3+4(m-5) log _{dfrac{1}{2}}dfrac{1}{x-2}+4m-4 có nghiệm thuộc [dfrac{5}{2};4]Bài 4: Cho phương trình (m-2)×log_{2} ^2 (x-4)-(2m+1)log_{dfrac{1}{2}} (x-4)+m+20. Tìm m để phương trình có 2 nghiệm phân biệt x1, x2 thỏa mãn...
Đọc tiếp
Bài 1: Phương trình\(\log_{2} ^3(x-1)-27y^3+8^y+1-x\) có bao nhiêu \((x;y)\) nghiệm thuộc \([8^{1992}; 8^{2020}]\)
Bài 2: Tìm tập hợp số thực m để phương trình \(2^{2x-1}+m×2^x+2m-2=0\) có 2 nghiệm thực phân biệt thuộc đoạn [1;2]
Bài 3: Tìm các số nguyên m để phương trình \(\log_{\dfrac{1}{2}}^{2} (x-2)^3+4(m-5) log _{\dfrac{1}{2}}\dfrac{1}{x-2}+4m-4\) có nghiệm thuộc \([\dfrac{5}{2};4]\)
Bài 4: Cho phương trình \((m-2)×log_{2} ^2 (x-4)-(2m+1)log_{\dfrac{1}{2}} (x-4)+m+2=0.\) Tìm m để phương trình có 2 nghiệm phân biệt x1, x2 thỏa mãn 4<x1, x2<6
Phương trình lg(x-3) + lg(x-2) =1- lg5 có tất cả bao nhiêu nghiệm trên tập số thực.
A. 2
B. 3
C . 1
D. 4
Chọn D.
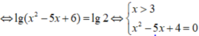
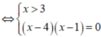
<=> x = 4
Vậy phương trình đã cho có nghiệm duy nhất là x= 4
Đúng 0
Bình luận (0)
Phương trình lg( x - 3) + lg( x - 2) = 1 - lg5 có tất cả bao nhiêu nghiệm trên tập số thực.
A. 2
B. 3
C . 1
D. 4
Chọn C.
Điều kiện: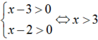 
Phương trình đã cho tương đương với:
lg( x - 3) (x - 2) = lg10 - lg 5 = lg2
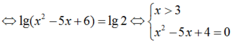
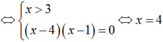
Vậy phương trình đã cho có nghiệm duy nhất là x = 4.
Đúng 0
Bình luận (0)
Cho hàm số
f
(
x
)
x
3
-
3
x
2
+
x
+
3
/
2
. Phương trình
f
f
x...
Đọc tiếp
Cho hàm số f ( x ) = x 3 - 3 x 2 + x + 3 / 2 . Phương trình f f x 2 f x - 1 = 1 có bao nhiêu nghiệm thực phân biệt?
A. 9
B. 6
C. 5
D. 4
Đáp án C
Điều kiện: 
.
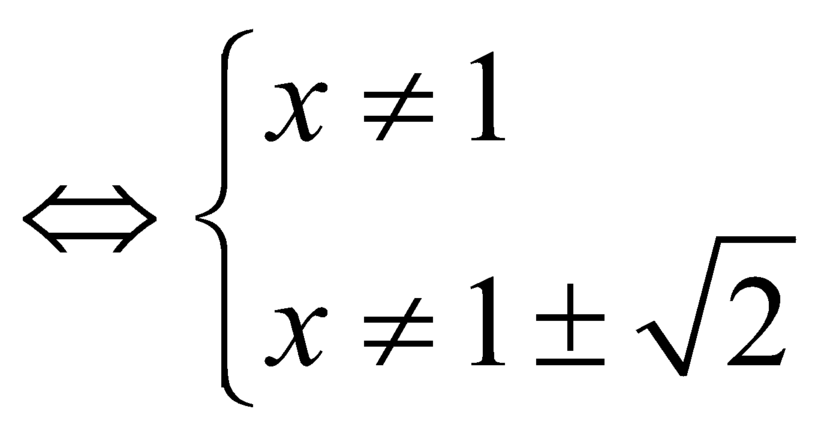Xét hàm số 
có 
; 
.
Chia 
cho 
ta được:
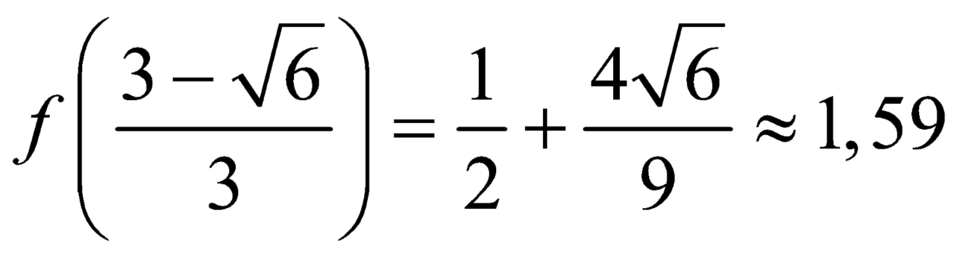
Bảng biến thiên và đồ thị:
Đặt 
.
Phương trình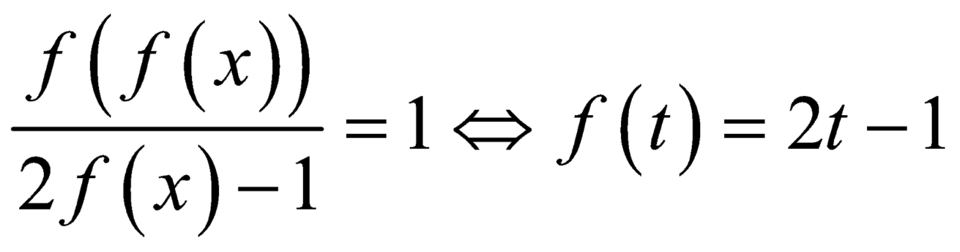 
.
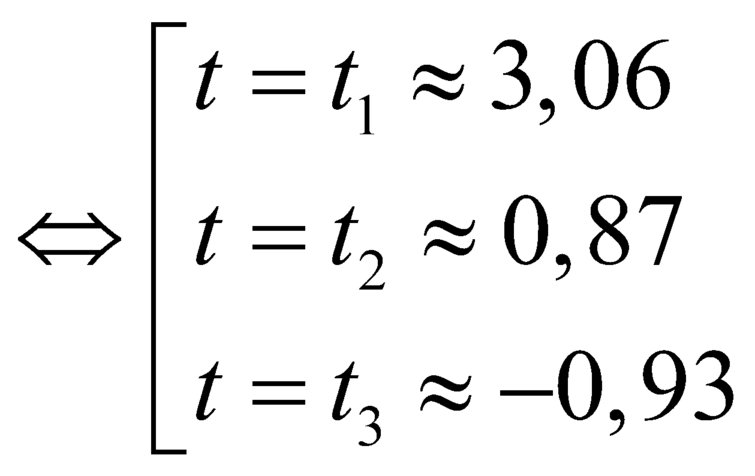
Với 
, từ đồ thị ta thấy phương trình này chỉ cho 1 nghiệm.
Với 
, từ đồ thị ta thấy phương trình này cho 3 nghiệm.
Với 
, từ đồ thị ta thấy phương trình này chỉ cho 1 nghiệm.
Vậy phương trình đã cho có 5 nghiệm phân biệt.
Đúng 0
Bình luận (0)
Cho phương trình \(x^2-2x-2\left|x-m\right|+1=0\) Có bao nhiêu giá trị của tham số m để có 3 nghiệm thực phân biệt
Có bao nhiêu số nguyên m để phương trình
ln
m
+
2
sin
x
+
ln
m
+
3
sin
x
sin
x
có nghiệm thực ? A. 4. B. 3. C. 5. D. 6.
Đọc tiếp
Có bao nhiêu số nguyên m để phương trình ln m + 2 sin x + ln m + 3 sin x = sin x có nghiệm thực ?
A. 4.
B. 3.
C. 5.
D. 6.
Phương trình lg4(x - 1) 2 + lg2(x - 1) 3 25 có bao nhiêu nghiệm ? A. 2 B. 3 C. 4 D. 5
Đọc tiếp
Phương trình lg4(x - 1) 2 + lg2(x - 1) 3 = 25 có bao nhiêu nghiệm ?
A. 2
B. 3
C. 4
D. 5
Có bao nhiêu giá trị nguyên của tham số m để phương trình
6
+
x
-
2
-
x
-
3
+
x
-
6
-
x
-
5
-
m
0
có nghiệm thực A. 0 B. 2 C. 3 D. 1
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để phương trình 6 + x - 2 - x - 3 + x - 6 - x - 5 - m = 0 có nghiệm thực
A. 0
B. 2
C. 3
D. 1
1. Cho phương trình: $x^{2}+m x-m-10$ ( $m$ là tham số). Tìm $m$ để phương trình có 2 nghiệm $x_{1} ; x_{2}$ thỏa mãn: $left|x_{1}-x_{2}right|2$.
2.Một nhóm học sinh dự định đóng góp $300$ cuốn vở để làm quà tặng cho các em nhỏ có hoàn cảnh khó khăn ờ một mái ấm tình thương. Thực tế ngày đi trao quà có thêm $2$ bạn tham gia đi cùng với nhóm và mỗi bạn trong nhóm góp nhiều hơn dự định $1$ cuốn vở, nên tổng số vở góp được là $351$ cuốn. Hỏi ban đầu nhóm đó có bao nhiêu học sinh và mỗi học sinh dự...
Đọc tiếp
1. Cho phương trình: $x^{2}+m x-m-1=0$ ( $m$ là tham số). Tìm $m$ để phương trình có 2 nghiệm $x_{1} ; x_{2}$ thỏa mãn: $\left|x_{1}-x_{2}\right|=2$.
2.Một nhóm học sinh dự định đóng góp $300$ cuốn vở để làm quà tặng cho các em nhỏ có hoàn cảnh khó khăn ờ một mái ấm tình thương. Thực tế ngày đi trao quà có thêm $2$ bạn tham gia đi cùng với nhóm và mỗi bạn trong nhóm góp nhiều hơn dự định $1$ cuốn vở, nên tổng số vở góp được là $351$ cuốn. Hỏi ban đầu nhóm đó có bao nhiêu học sinh và mỗi học sinh dự định góp bao nhiêu cuốn vở. (Biết rằng số vờ mỗi học sinh đóng góp là như nhau).
3. Giải phương trình: $ 2 x^{2}-3 x-2=(x-2) \sqrt{3 x^{2}+x+5}$.
1) Giải phương trình: x(x-3)-(x+2)(x-1)=3 ta được nghiệm
2) Phương trình nào sau đây có 1 nghiệm
a) x(x-1)=0 b) (x+2)(x2+1)=0
c) x2-3x=0 d) x2-2x+3=0
1. x(x-3)-(x+2)(x-1)=3 <=> x2 - 3x - x2 - x + 2 = 3 => 4x = -1 => x = 1/4
2.
a) x = 0, x=1 (2 nghiệm, loại)
b) x2 + 1 > 0 => x = - 2 (1 nghiệm, chọn b)
c) <=> x(x-3) = 0 => x = 0, x=3 (2 nghiệm, loại)
d) (x-1)2 + 2 > 0 => Vô nghiệm (loại)
Đúng 0
Bình luận (0)