Cho các số thực x,y thoả mãn điều kiện x2+5y2+2y-4xy-3=0
Chứng Minh Rằng : |x-2y| \(\le\) 2
tìm tất cả các cặp số thực (x;y) sao cho y là số nhỏ nhất thoả mãn điều kiện \(x^2+5y^2+2y+4xy-3=0\)
\(x^2+5y^2+2y+4xy-3=0\)
\(\Leftrightarrow\)\((x^2+4xy+4y^2)+(y^2+2y+1)=4\)
\(\Leftrightarrow\)\((x+2y)^2+(y+1)^2=4\)
\(\Leftrightarrow\)\((x+2y)^2=4-(y+1)^2\)
\(\Leftrightarrow\)\((x+2y)^2=(2-y-1)(2+y+1)\)
\(\Leftrightarrow\)\((x+2y)^2=(1-y)(3+y)\)
\(Vì \) \((x+2y)^2\geq0\)
\(\Rightarrow\)\((1-y)(3+y)\geq0\)
\(\Rightarrow\)\(\left[\begin{array}{}
\begin{cases}
1-y\geq0\\
3+y\geq0
\end{cases}\\
\begin{cases}
1-y\leq0\\
3+y\leq0
\end{cases}
\end{array} \right.\)
\(\Rightarrow\)\(\left[\begin{array}{}
\begin{cases}
y\leq1\\
y\geq-3
\end{cases}\\
\begin{cases}
y\geq1\text{(Vô lí)}\\
y\leq-3\text{(Vô lí)}
\end{cases}
\end{array} \right.\)\(\Rightarrow\)\(-3\leq y\leq1\)
\(\text{Mà y là số nhỏ nhất}\)
\(\Rightarrow\)\(y=-3\)
\(\Rightarrow\)\(x+2.(-3)=0\text{ (Vì }(x+2y)^2\geq0)\)
\(\Rightarrow\)\(x=6\)
\(\text{Vậy cặp số (x,y) thỏa mãn yêu cầu bài toán là: (6;-3)}\)
Nếu mình đúng cho mình xin 1 like nha
Bài 3: (2,0 điểm)
1. Cho x, y là các số thực thoả mãn điều kiện: x2 + 5y2 – 4xy – x + 2y – 6 = 0. Chứng minh: -1≤x-2y+1≤4
Tìm nghiệm nguyên của phương trình: y3 – x3 = 2x + 1
\(x^2+4y^2+\frac{1}{4}-4xy-x+2y+y^2-\frac{25}{4}=0\)
\(\Leftrightarrow\left(x-2y-\frac{1}{2}\right)^2=\frac{25}{4}-y^2\le\frac{25}{4}\)
\(\Rightarrow\frac{-5}{2}\le x-2y-\frac{1}{2}\le\frac{5}{2}\)
\(\Rightarrow-2\le x-2y\le3\)
\(\Rightarrow-1\le x-2y+1\le4\) (đpcm)
Dấu "=" xảy ra khi \(y=0\) và \(x=...\)
2/ \(x^3+2x+1=y^3\)
- Với \(x=0\Rightarrow y=1\)
\(VT=x^3+3x^2+3x+1-3x^2-x=\left(x+1\right)^3-x\left(3x+1\right)\) (1)
Do \(x\left(3x-1\right)\ge0\) \(\forall x\in Z\)
\(\Rightarrow VT\le\left(x+1\right)^3\Rightarrow y^3\le\left(x+1\right)^3\Rightarrow y\le x+1\)
Lại có:
\(VT=x^3-3x^2+3x-1+3x^2-x+2=\left(x-1\right)^3+3x^2-x+2\)
Do \(3x^2-x+2>0\) \(\forall x\Rightarrow VT>\left(x-1\right)^3\Rightarrow y^3>\left(x-1\right)^3\Rightarrow y>x-1\)
\(\Rightarrow x-1< y\le x+1\Rightarrow\left[{}\begin{matrix}y=x\\y=x+1\end{matrix}\right.\)
- Với \(y=x\) thay vào pt ta được: \(2x+1=0\Rightarrow x=\frac{-1}{2}\left(ktm\right)\)
- Với \(y=x+1\) từ \(\left(1\right)\Rightarrow x\left(3x+1\right)=0\Rightarrow\left\{{}\begin{matrix}x=0\\y=1\end{matrix}\right.\)
Vậy \(\left(x;y\right)=\left(0;1\right)\) là cặp nghiệm nguyên duy nhất
cho các số thực x,y,z thỏa mãn \(\left(x-y +z\right)^2\)+\(\sqrt{y^4}\)+\(\left|1-z^3\right|\) \(\le\) 0
Chứng minh rằng \(x^{2023}\)+\(y^{2024}\)+\(z^{2025}\)=0
Lời giải:
Ta thấy, với mọi $x,y,z$ là số thực thì:
$(x-y+z)^2\geq 0$
$\sqrt{y^4}\geq 0$
$|1-z^3|\geq 0$
$\Rightarrow (x-y+z)^2+\sqrt{y^4}+|1-z^3|\geq 0$ với mọi $x,y,z$
Kết hợp $(x-y+z)^2+\sqrt{y^4}+|1-z^3|\leq 0$
$\Rightarrow (x-y+z)^2+\sqrt{y^4}+|1-z^3|=0$
Điều này xảy ra khi: $x-y+z=y^4=1-z^3=0$
$\Leftrightarrow y=0; z=1; x=-1$
Tìm các cặp số nguyên dương (x;y) thoả mãn 1 trong các điều kiện sau: 1)2x+2y-3 chia hết cho xy
2)x+2y+1 chia hết cho xy
Bài 4:Cho các số x,y thoả mãn đẳng thức 5x2+5y2+8xy-2x+2y+2=0
Tính giá trị của biểu thức:M=(x+y)2019 + (x-2)2020 + (y+1)2021
Cho x, y là hai số thực dương thỏa mãn điều kiện 4 + 9.3 x 2 − 2 y = 4 + 9 x 2 − 2 y .7 2 y − x 2 + 2 .Tìm giá trị nhỏ nhất của biểu thức P = x + 2 y + 18 x .
A. P = 3 + 2 2
B. P = 1 + 9 2
C. P = 9
D. Không tồn tại
Cho x, y là hai số thực dương thỏa mãn điều kiện 4 + 9 . 3 x 2 - 2 y = ( 4 + 9 x 2 - 2 y ) . 7 2 y - x 2 + 2 .Tìm giá trị nhỏ nhất của biểu thức P = x + 2 y + 18 x .
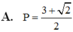
![]()
![]()
D. Không tồn tại
Cho \(y\)là các số thực thỏa mãn điều kiện \(1-2y-y^2\ge0\). Chứng minh rằng
\(\sqrt{1-2y-y^2}\le y+3\)
Dấu đẳng thức xảy ra khi nào?
đk: \(y+3\ge0\)
BĐT cần chứng minh tương đương
\(BPT\Leftrightarrow1-2y-y^2\le\left(y+3\right)^2=y^2+6y+9\)
\(\Leftrightarrow2y^2+8y+8\ge0\)
\(\Leftrightarrow2\left(y+2\right)^2\ge0\left(\forall y\right)\)
Dấu "=" xảy ra khi: \(y+2=0\Rightarrow y=-2\)
Xét các số thực dương x,y thoả mãn điều kiện x3 + y3 +(x + y)3 + 30xy = 2000. Chứng minh rằng x +y =10
\(\Leftrightarrow\left(x+y\right)^3-3xy\left(x+y\right)+\left(x+y\right)^3+30xy=2000\)
\(\Leftrightarrow2\left[\left(x+y\right)^3-1000\right]-3xy\left(x+y-10\right)=0\)
\(\Leftrightarrow2\left(x+y-10\right)\left[\left(x+y\right)^2-10\left(x+y\right)+100\right]-3xy\left(x+y-10\right)=0\)
\(\Leftrightarrow\left(x+y-10\right)\left[2\left(x+y\right)^2-20\left(x+y\right)+200-3xy\right]=0\)
\(\Leftrightarrow x+y=10\)
Do:
\(2\left(x+y\right)^2-20\left(x+y\right)+200-3xy\)
\(=\left(x+y-10\right)^2+\left(x+y\right)^2-3xy+100\)
\(=\left(x+y-10\right)^2+\left(x+\dfrac{y}{2}\right)^2+\dfrac{3y^2}{4}+100>0\)