cho tam giác ABC có H là trung điểm AB và G thuộc AC ; GC=2AG. F là giao của CH và BG. Tìm điểm I trên Bc sao cho I,F,A thẳng hàng( cm theo véc tơ giúp mình với ạ)

Những câu hỏi liên quan
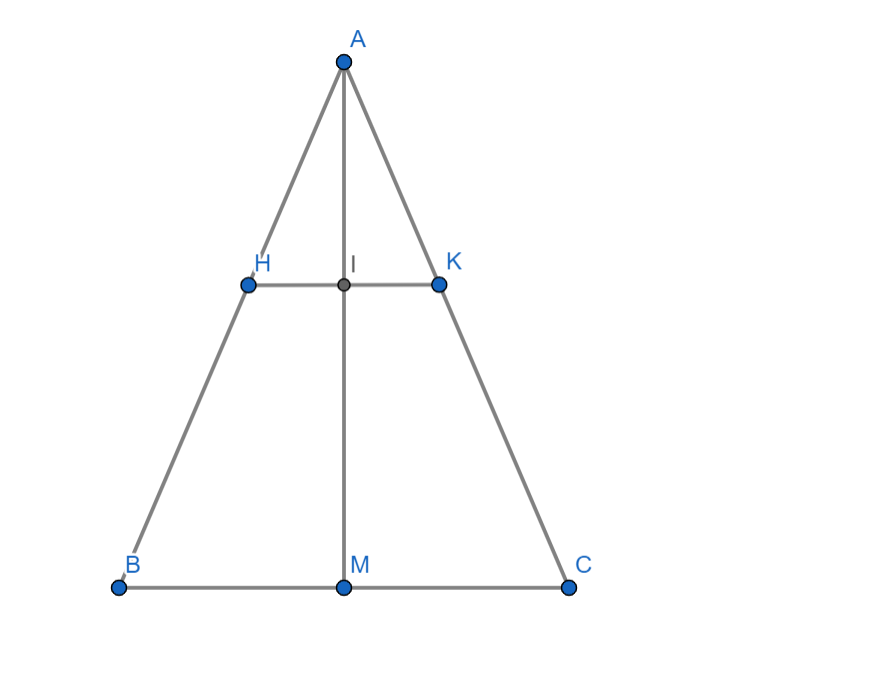
Cho tam giác ABC có AB=AC, M là trung điểm BC.Gọi điểm H thuộc AB và điểm K thuộc AC sao cho AH=AK.Gọi I là giao điểm của AM và HK.
Ai help vẽ hình với
Cho tam giác ABC có AC = 2 AB và AD là đường phân giác gọi M là trung điểm AC và E là trung điểm ah AM, AD cắt BE tại G chứng minh rằng 1) tam giác ABC đồng dạng tam giác AEB 2)G là trọng tâm tam giác ABM 3) tứ giác BGMD là h thoi
Cho tam giác ABC có AC = 2 AB và AD là đường phân giác gọi M là trung điểm AC và E là trung điểm ah AM, AD cắt BE tại G chứng minh rằng 1) tam giác ABC đồng dạng tam giác AEB 2)G là trọng tâm tam giác ABM 3) tứ giác BGMD là h thoi
cho tam giác abc cân tại a h là trung điểm của bc. kẻ hm vuông góc ab ( m thuộc ab), hn vuông góc với ac (n thuộc ac)
a, chứng minh tam giác ahb = tam giác ahc
b, chứng minh tam giác hmn cân
c, chứng minh mn//bc
d, gọi e là giao điểm của ab và hn, f là giao điểm của ac và hm, i là giao điểm của ah và ef, chứng minh điểm h cách đều 3 cạnh tam giác mni
a: Xet ΔAHB và ΔAHC có
AB=AC
AH chung
HB=HC
=>ΔAHB=ΔAHC
b: Xet ΔAMH vuông tại M và ΔANH vuông tại N co
AH chung
góc MAH=góc NAH
=>ΔAMH=ΔANH
=>AM=AN và HM=HN
=>ΔHMN cân tại H
c: Xét ΔABC có AM/AB=AN/AC
nên MN//CB
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có đường trung tuyến AM. Kẻ MH, MK lần lượt vuông góc với AB và AC (H thuộc AB và K thuộc AC).b) Chứng minh tứ giác BHKM là hình bình hànhc) Gọi E là trung điểm của MH, gọi F là trung điểm của MK. Đường thẳng HK cắt AE, AF lần lượt tại I và J. Chứng minh HI KJ.d) Gọi G là trọng tâm tam giác ABC. Giả sử tam giác ABG vuông tại G và AB 43 (cm). Tính độ dài EF.
Đọc tiếp
Cho tam giác ABC vuông tại A có đường trung tuyến AM. Kẻ MH, MK lần lượt vuông góc với AB và AC (H thuộc AB và K thuộc AC).
b) Chứng minh tứ giác BHKM là hình bình hành
c) Gọi E là trung điểm của MH, gọi F là trung điểm của MK. Đường thẳng HK cắt AE, AF lần lượt tại I và J. Chứng minh HI = KJ.
d) Gọi G là trọng tâm tam giác ABC. Giả sử tam giác ABG vuông tại G và AB = 43 (cm). Tính độ dài EF.
Cho tam giác ABC cân tại A, đường cao AH (H thuộc BC)
a, Chứng minh Tam giác ABH= Tam giác ACH
b,Từ H kẻ MH, HN lần lượt vuông góc với AB và AC (M thuộc AB) (N thuộc AC). Chứng minh HM=HN
c, Gọi G là giao điểm của hai trung tuyến BE và CF của tam giác ABC (E thuộc AC) (F thuộc AB)
Làm nhanh mk tick!
a) Xét tam giác ABH vuông tại H và tam giác ACH vuông tại H có:
AB=AC(tam giác ABC cân tại A)
AH: chung
Do đó:tam giác ABH= tam giác ACH(ch-cgv)
b)Xét tam giác BMH vuông tại M và tam giác CNH vuông tại N có:
BH=CH(tam giác ABH=tam giác ACH)
góc B=góc C(tam giác ABC cân tại A)
Do đó:tam giác BMH=tam giác CNH(ch-gn)
#Ở câu b bạn có thể chọn trường hợp ch-cgv cũng đc hjhj:)))<3#
c)bn cho thiếu dữ kiên nên mk k làm đc nhé tks
P/S: chúc bạn học tốt..........boaiiii>.< moa<3
Đúng 0
Bình luận (0)
Bài 2. Cho tam giác ABC vuông tại A có AD là đường trung tuyến. Kẻ DH // AC và DK // AB (H thuộc AB, K thuộc AC)
a) Chứng minh H là trung điểm của AB và K là trung điểm của AC
b) Chứng minh AHDK là hình chữ nhật
a: Xét ΔABC có
D là trung điểm của BC
DH//AC
Do đó: H là trung điểm của AB
Xét ΔABC có
D là trung điểm của BC
DK//AB
Do đó: K là trung điểm của AC
Đúng 0
Bình luận (0)
Cho tam giác ABC đều, có AH là đường cao và M là điểm bất kì thuộc đoạn BC. Kẻ MP và MQ lần lượt vuông góc với AB và AC. Gọi O là trung điểm của AM. Gọi G là trọng tâm tam giác ABC, I là giao điểm của PQ và OH. Chứng minh rằng: 3 điểm M, I, G thẳng hàng
Bài 9 (1 điểm) Cho tam giác ABC có M là điểm thuộc cạnh BC sao cho BC 3 x MC và N là điểm thuộc cạnh AC sao cho AC 4 x AN. Kéo dài MN cắt AB kéo dài tại P. Tính tỉ số diện tích tam giác PAN và tam giác ABC.Bài 10 (1 điểm) Cho tam giác ABC có M là trung điểm AB. N là điểm thuộc cạnh AC sao cho AC 3 x NC. Gọi P là trung điểm AN, Q là trung điểm MN. Tính diện tích tam giác PQN biết diện tích tam giác ABC là 180cm2.1 điểm
Đọc tiếp
Bài 9 (1 điểm) Cho tam giác ABC có M là điểm thuộc cạnh BC sao cho BC = 3 x MC và N là điểm thuộc cạnh AC sao cho AC = 4 x AN. Kéo dài MN cắt AB kéo dài tại P. Tính tỉ số diện tích tam giác PAN và tam giác ABC.
Bài 10 (1 điểm) Cho tam giác ABC có M là trung điểm AB. N là điểm thuộc cạnh AC sao cho AC = 3 x NC. Gọi P là trung điểm AN, Q là trung điểm MN. Tính diện tích tam giác PQN biết diện tích tam giác ABC là 180cm2.
1 điểm
giúp mik nhé, mik đang cần gấp
Bài 4: Cho tam giác ABC có N là trung điểm của AC. Qua N kẻ MN//BC (M thuộc cạnh BC), NP//AB (P thuộc BC)
a.Chứng minh tứ giác MNPB là hình bình hành và P là trung điểm BC
b.Gọi H đối xứng với P qua M. Chứng minh HB//AP
c.Gọi I là trung điểm HB và O giao điểm của AP và MN. Chứng minh I, O, N thẳng hàng.
a: Xét tứ giác MNPB có
MN//BP
MB//NP
Do đó: MNPB là hình bình hành
Đúng 0
Bình luận (1)