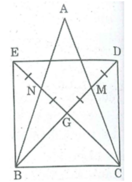
Cho \(\Delta ABC\) cân tại A. Gọi BD, CE là hai trung tuyến của tam giá ABC cắt nhau tại G. Gọi M là điểm đối xứng với G qua E. Gọi N là điểm đối xứng với G qua D
a) Tứ giác EDNM là hình gì? vì sao?
b) tứ giác MNCB là hình gì ? vì sao?
c) CMR: Tứ giác AMBN là hình thang
d) tìm điều kiện của tam giác ABC để AMBN là hình thang cân
Cho tam giác ABC cân tại A, các đường trung tuyến BM, CN cắt nhau tại G. Gọi D là điểm đối xứng với G qua M, gọi E là điểm đối xứng với G qua N. Tứ giác BEDC là hình gì? Vì sao?
* Tam giác ABC có hai đường trung tuyến BM và CN cắt nhau tại G
Suy ra: G là trọng tâm của ∆ ABC .
⇒ GB = 2GM (tính chất đường trung tuyến)
GC = 2GN (tính chất đường trung tuyến)
Điểm D đối xứng với điểm G qua điểm M
⇒ MG = MD hay GD = 2GM
Suy ra: GB = GD (l)
Điểm E đối xứng với điểm G qua điểm N
⇒ NG = NE hay GE = 2GN
Suy ra: GC = GE (2)
Từ (1) và (2) suy ra tứ giác BCDE là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)
Xét ∆ BCM và ∆ CBN, có: BC cạnh chung
∠ (BCM) = ∠ (CBN) (tính chất tam giác cân)
CM = BN (vì AB = AC)
Suy ra: ∆ BCM = ∆ CBN (c.g.c)
⇒ ∠ (MBC) = ∠ (NCB) ⇒ ∆ GBC cân tại G ⇒ GB = GC ⇒ BD = CE
Hình bình hành BCDE có hai đường chéo bằng nhau nên nó là hình chữ nhật.
Cho tam giác ABC cân tại A, các đường trung tuyến BM, CN cắt nhau tại G. Gọi D là điểm đối xứng với G qua M, gọi E là điểm đối xứng với G qua N. Tứ giác BEDC là hình gì ? Vì sao ?
Cho tam giác ABC cân tại A, các đường trung tuyến BM, CN cắt nhau tại G. Gọi
D là điểm đối xứng với G qua M, gọi E là điểm đối xứng với G qua N. Tứ giác BEDC là
hình gì? Vì sao?
Cho tam giác ABC, trung tuyến BM, CN cắt nhau tại G. Gọi P là điểm đối xứng của M qua G. Gọi Q là điểm đối xứng của N qua G. a) Tứ giác MNPQ là hình gì? Vì sao? b) Nếu tam giác BAC cân tại A thì tứ giác MNPQ là hình gì? Vì sao?
Cho tam giác ABC, các trung tuyến BM và CN cắt nhau tại G. Gọi P là điểm đối xứng của M qua G; gọi Q là điểm đối xứng của N qua G.
a) Tứ giác MNPQ là hình gì? Vì sao?
b) Nếu tam giác ABC cân tại A thì tứ giác MNPQ hình gì? vì sao? help me
a)
Xét tứ giác MNPQ có
G là trung điểm của đường chéo MP(gt)
G là trung điểm của đường chéo NQ(gt)
Do đó: MNPQ là hình bình hành(Dấu hiệu nhận biết hình bình hành)
b)
Xét ΔABC có
BM là đường trung tuyến ứng với cạnh AC(gt)
CN là đường trung tuyến ứng với cạnh AB(gt)
BM cắt CN tại G(gt)
Do đó: G là trọng tâm của ΔABC(Định lí ba đường trung tuyến của tam giác)
Suy ra: \(MG=\dfrac{1}{3}MB;BG=\dfrac{2}{3}MB;NG=\dfrac{1}{3}NC;CG=\dfrac{2}{3}NC\)(1)
Ta có: G là trung điểm của MP(gt)
nên MG=GP
mà \(MG=\dfrac{1}{3}MB\)
nên \(MG=GP=\dfrac{1}{3}MB\)
Ta có: MG+GP=MP(G nằm giữa M và P)
nên \(MP=\dfrac{1}{3}MB+\dfrac{1}{3}MB=\dfrac{2}{3}MB\)(1)
Ta có: G là trung điểm của NQ(gt)
nên \(GN=GQ=\dfrac{1}{3}NC\)
Ta có: NG+GQ=NQ(G là trung điểm của NQ)
nên \(NQ=\dfrac{1}{3}NC+\dfrac{1}{3}NC=\dfrac{2}{3}NC\)(2)
Ta có: \(AN=NB=\dfrac{AB}{2}\)(N là trung điểm của AB)
\(AM=MC=\dfrac{AC}{2}\)(M là trung điểm của AC)
mà AB=AC(ΔBAC cân tại A)
nên AN=NB=AM=MC
Xét ΔAMB và ΔANC có
AB=AC(ΔABC cân tại A)
\(\widehat{BAM}\) chung
AM=AN(cmt)
Do đó: ΔAMB=ΔANC(c-g-c)
Suy ra: BM=CN(hai cạnh tương ứng)(3)
Từ (1), (2) và (3) suy ra NQ=MP
Hình bình hành MNPQ có NQ=MP(cmt)
nên MNPQ là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
Cho tam giác ABC các trung tuyến BM;CN cắt nhau tại G gọi P là điểm đối xứng của M qua G ;gọi Q là điểm đối xứng của N qua G
tứ giác MNPQ la hình gì ?
NẾU tam giác ABC cân ở A thì tứ giác MNPQ là hình gì ?vì sao
Cho tam giác ABC có hai đường trung tuyến BD và CE cắt nhau tại g Gọi M, N lần lượt là trung điểm của BG và CG
a) Chứng minh tứ giác bcde là hình vuông .
b) c/m tứ giác MNDE là hình bình hành
c) lấy k đối xứng với g qua b. c/m tứ giác ABCK là hbh
d) tam giác ABC có thêm điều kiện gì để tứ giác MNDE là hcn
Giúp mik vs cần gấp lắm ạ!!
b: Xét ΔABC có
E là trung điểm của AB
D là trung điểm của AC
Do đó: ED là đường trung bình của ΔABC
Suy ra: ED//BC và \(ED=\dfrac{BC}{2}\left(1\right)\)
Xét ΔGBC có
M là trung điểm của GB
N là trung điểm của GC
Do đó: NM là đường trung bình của ΔGBC
Suy ra: MN//BC và \(MN=\dfrac{BC}{2}\left(2\right)\)
Từ (1) và (2) suy ra ED//MN và ED=MN
hay MNDE là hình bình hành
Cho tam giác ABC cân tại A, các đường trung tuyến BM, CN cắt nhau tại G. Gọi D là điiểm đối xứng G qua M, E đối xứng G qua N. Tứ giác BEDC là hình gì? Vì sao?
Tự vẽ hình:
cminh:Vì D đối xứng với G qua M
=>GM=MD Hay GD=2GM
Vì BM;CN cắt nhau tại G trong tam giác ABC
=>G là trọng tâm trong Tam giác ABC =>BG=2GM
Suy ra : GD=BG(vì =2GM)=> G là trung điểm của BD (1)
Ta lại có : E đối xứng với G qua N=> EN=GN Hay EG=2NG
Và CG=2GN( G là trọng tâm)
Suy ra: CG=EG ( vì =2NG) (2) (*)
Từ (1) (2)=> Tứ giác BEDC là hình bình hành
Xét \(\Delta\)CBM Và \(\Delta\)BCN Có:
BC: Cạnh chung
Góc B=C(g/t)
BN=CM(AB=AC)
=> hai tam giác bằng nhau(c-g-c)
=>MBC=NCB(2 góc tương ứng) hay tam giác GBC cân=> BG=GC (**)
Từ (*) (**)=> Hình bình hành BEDC là hình chữ nhật
