Question

Cho tam giác ABC cân tại A, các đường trung tuyến BM, CN cắt nhau tại G. Gọi D là điểm đối xứng với G qua M, gọi E là điểm đối xứng với G qua N. Tứ giác BEDC là hình gì? Vì sao?

Answer 1

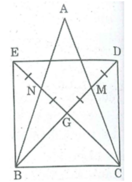
* Tam giác ABC có hai đường trung tuyến BM và CN cắt nhau tại G

Suy ra: G là trọng tâm của ∆ ABC .

⇒ GB = 2GM (tính chất đường trung tuyến)

GC = 2GN (tính chất đường trung tuyến)

Điểm D đối xứng với điểm G qua điểm M

⇒ MG = MD hay GD = 2GM

Suy ra: GB = GD (l)

Điểm E đối xứng với điểm G qua điểm N

⇒ NG = NE hay GE = 2GN

Suy ra: GC = GE (2)

Từ (1) và (2) suy ra tứ giác BCDE là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)

Xét  ∆ BCM và  ∆ CBN, có: BC cạnh chung

∠ (BCM) =  ∠ (CBN) (tính chất tam giác cân)

CM = BN (vì AB = AC)

Suy ra:  ∆ BCM = ∆ CBN (c.g.c)

⇒  ∠ (MBC) =  ∠ (NCB) ⇒  ∆ GBC cân tại G ⇒ GB = GC ⇒ BD = CE

Hình bình hành BCDE có hai đường chéo bằng nhau nên nó là hình chữ nhật.