a) ABCD là hình thang vuông ( AD//BC)

Mà OM//AD //BC  và O là trung điểm AB

theo định lí về đường TB hình thang => M là trung điểm của DC => MD =MC

b) theo a => OM là đường TB của ABCD => OM = (AD+BC)/2 hay AD+BC = 2 OM = 2R = không đổi

c) M là trung điểm CD => (M;CD/2)  là đường tròn đường kính CD

C thuộc (M) mà BC _|_ CD tại C => BC là tiếp tuyến của (M)

D thuộc (M) mà AD_|_ CD tại D => AD là tiếp tuyến của (M)

d) do AD+BC =2R

=> S ( ABCD) lớn nhát khi CD lớn nhát => CD =AB = 2R 

khi đó M là điểm chính giữa cung AB

1. Ta có  AD // OM // BC ; OA = OB

=> OM là đường trung bình của hình thang ABCD => M là trung điểm CD => MC = MD

2. Vì OM là đường trung bình của hình thang ABCD nên : \(OM=\frac{AD+BC}{2}\Rightarrow AD+BC=2OM\)không đổi. 

3. Dễ thấy M là tâm của đường tròn đường kính CD vì MC = MD

Lại có AD vuông góc với MD => đpcm

4. Ta có : \(S_{ABCD}=\frac{1}{2}.\left(AD+BC\right).CD=OM.CD\)

Vì OM không đổi nên S.ABCD lớn nhất <=> CD lớn nhất <=> CD = AB

Vậy max (S.ABCD) = OM . AB = R.(2R) = 2R² với R = AB/2

Cần giải thì liên lạc face 0915694092 nhá

giúp tôi trả lời tất cả câu hỏi đề này cái

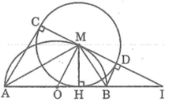
Trong đường tròn (M; MH), theo tính chất hai tiếp tuyến cắt nhau, ta có:

- MA là tia phân giác của góc HMC

Vậy C, M, D thẳng hàng.

a: Xét hình thang ABCD có 

O là trung điểm của AB

OM//AD//CB

Do đó: M là trung điểm của CD

hay MD=MC

a, 70⁰ góc nào bạn ? 

b, Vì AB là tiếp tuyến (O) => ^ABO = 90⁰ 

AO giao BC = K 

AB = AC ; OB = OC = R 

Vậy OA là đường trung trực đoạn BC 

Xét tam giác ABO vuông tại B, đường cao BK

Áp dụng định lí Pytago tam giác ABO vuông tại B 

\(AB=\sqrt{AO^2-BO^2}=\sqrt{16-4}=2\sqrt{3}\)cm 

Áp dụng hệ thức : \(BK.AO=BO.AB\Rightarrow BK=\frac{BO.AB}{AO}=\frac{4\sqrt{3}}{4}=\sqrt{3}\)cm 

Vì AO là đường trung trực => \(BC=2KB=2\sqrt{3}\)cm 

Chu vi tam giác ABC là :

 \(P_{ABC}=AB+AC+BC=2AB+BC=4\sqrt{3}+2\sqrt{3}=6\sqrt{3}\)cm 

bạn god rick giải dài nhưng chưa chắc là đúng

a) Xét tứ giác AOMC có

ˆCAOCAO^ và ˆCMOCMO^ là hai góc đối

ˆCAO+ˆCMO=1800(900+900=1800)CAO^+CMO^=1800(900+900=1800)

Do đó: AOMC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

b) Ta có: AOMC là tứ giác nội tiếp(cmt)

nên ˆMAO=ˆOCMMAO^=OCM^(hai góc cùng nhìn cạnh OM)

hay ˆMAB=ˆOCDMAB^=OCD^

Xét (O) có

CM là tiếp tuyến có M là tiếp điểm(Gt)

CA là tiếp tuyến có A là tiếp điểm(Gt)

Do đó: OC là tia phân giác của ˆAOMAOM^(Tính chất hai tiếp tuyến cắt nhau)

⇔ˆAOM=2⋅ˆCOM⇔AOM^=2⋅COM^

Xét (O) có

DM là tiếp tuyến có M là tiếp điểm(gt)

DB là tiếp tuyến có B là tiếp điểm(gt)

Do đó: OD là tia phân giác của ˆMOBMOB^(Tính chất hai tiếp tuyến cắt nhau)

⇔ˆBOM=2⋅ˆMOD⇔BOM^=2⋅MOD^

Ta có: ˆAOM+ˆBOM=1800AOM^+BOM^=1800(hai góc kề bù) 

mà ˆAOM=2⋅ˆCOMAOM^=2⋅COM^(cmt)

và ˆBOM=2⋅ˆMODBOM^=2⋅MOD^(cmt)

nên 2⋅ˆCOM+2⋅ˆMOD=18002⋅COM^+2⋅MOD^=1800

⇔ˆCOM+ˆMOD=900⇔COM^+MOD^=900

mà ˆCOM+ˆMOD=ˆCODCOM^+MOD^=COD^(tia OM nằm giữa hai tia OC,OD)

nên ˆCOD=900COD^=900

Xét ΔCOD có ˆCOD=900COD^=900(cmt)

nên ΔCOD vuông tại O(Định nghĩa tam giác vuông)

Xét (O) có

ΔMAB nội tiếp đường tròn(M,A,B∈(O))

AB là đường kính(gt)

Do đó: ΔMAB vuông tại M(Định lí)

Xét ΔAMB vuông tại M và ΔCOD vuông tại O có

ˆMAB=ˆOCDMAB^=OCD^(cmt)

Do đó: ΔAMB∼ΔCOD(g-g)

⇔AMCO=BMDOAMCO=BMDO(Các cặp cạnh tương ứng tỉ lệ)

hay AM⋅OD=BM⋅OCAM⋅OD=BM⋅OC(đpcm)