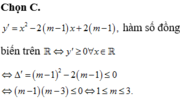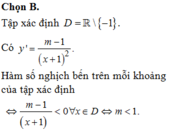tìm tất cả các giá trị của m để hàm số y= \(\frac{x^2+10}{x^2-m}\) xác định trên đoạn [-3;2]

Những câu hỏi liên quan
Tìm tất cả các giá trị của tham số m để tập xác định của hàm số
y = m x - 2 - x + 1 là một đoạn trên trục số.
A. m<-2
B. m>-2
C. m>2
D. m<2
tìm tập tất cả các giá trị của tham số m để hàm số y= -1/3x^3-(m-2)x^2+(m-2)x+m luôn nghịch biến trên tập xác định
\(y'=-x^2-2\left(m-2\right)x+m-2\)
Hàm nghịch biến trên TXĐ khi và chỉ khi \(y'\le0;\forall x\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=-1< 0\left(đúng\right)\\\Delta'=\left(m-2\right)^2+m-2\le0\end{matrix}\right.\)
\(\Leftrightarrow\left(m-2\right)\left(m-1\right)\le0\)
\(\Leftrightarrow1\le m\le2\)
Đúng 1
Bình luận (0)
1,Tìm tất cả các giá trị của m để hàm số y2x^2 - 3mx + m - 2 trên x-1 đạt cực đại tại điểm x2.
2, Tìm tất cả các giá trị của m để hàm số y x^2 + mx +1 trên x+m đạt cực tiểu tại điểm x2.
3, Tìm tất cả các giá trị của m để hàm số yx^2 -(2m-1)x+3 trên x+2 có cực đại và cực tiểu .
4, Tìm m để hso yx^2 +m(m^2-1)x-m^4+1 trên x-m có cực đại và cực tiểu.
Mọi người giúp em với ạ . Em cảm ơn ạ !
Đọc tiếp
1,Tìm tất cả các giá trị của m để hàm số y=2x^2 - 3mx + m - 2 trên x-1 đạt cực đại tại điểm x=2. 2, Tìm tất cả các giá trị của m để hàm số y= x^2 + mx +1 trên x+m đạt cực tiểu tại điểm x=2. 3, Tìm tất cả các giá trị của m để hàm số y=x^2 -(2m-1)x+3 trên x+2 có cực đại và cực tiểu . 4, Tìm m để hso y=x^2 +m(m^2-1)x-m^4+1 trên x-m có cực đại và cực tiểu. Mọi người giúp em với ạ . Em cảm ơn ạ !
Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\frac{mx}{\sqrt{x-m+2}-1}\)xác định trên (0;1)
Câu 1:Cho hàm số y= 4xmũ2 -4mx + mmũ2 – 2m . X xác định tất cả các giá trị của m để giá trị nhỏ nhất của hàm số trên đoạn [-2,0] bằng 3.
Câu 2: Cho parabol (P) : y= xmũ2 -4x =m (m là tham số) . Tìm tất cả các giá trị của m sao cho (P) cắt trục Ox tại điểm phân biệt A,B với OA = 3OB
Tìm tất cả các giá trị của tham số m để hàm số
y
1
m
log
3
2
x
-
4
log
3
x
+
...
Đọc tiếp
Tìm tất cả các giá trị của tham số m để hàm số y = 1 m log 3 2 x - 4 log 3 x + m + 3 xác định trên khoảng ( 0 ; + ∞ )
A . m ∈ - ∞ ; - 4 ∪ ( 1 ; + ∞ )
B . m ∈ ( 1 ; + ∞ )
A . m ∈ - ∞ ; - 4 ∪ ( 1 ; + ∞ )
C . m ∈ ( - ∞ ; - 4 )
Chọn A
Cách 1
Điều kiện: x > 0
Hàm số xác định khi:
![]()
![]()
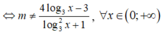
Để hàm số xác định trên
(
0
;
+
∞
)
thì phương trình 
Xét hàm số 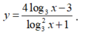
Đặt ![]() khi đó ta có
khi đó ta có
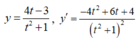
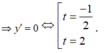
Ta có BBT:
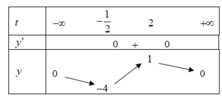
Để hàm số xác định trên ![]()
Cách 2:
Đề hàm số xác định trên khoảng ![]() thi phương trình
thi phương trình ![]() vô nghiệm.
vô nghiệm.
TH1: m = 0 thì PT trở thành ![]()
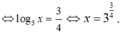
Vậy m = 0 không thỏa mãn.
TH2:
m
≠
0 thì để PT vô nghiệm ![]()
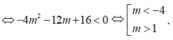
Để hàm số xác định trên ![]()
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của m để hàm số
y
x
3
3
–
(
m
-
1
)
x
2
+
2
(
m
-
1
)
x
+
2
đồng biến trên tập xác định của nó là: A. 1 m 3 B. m ≥ 1 C. 1 ≤ m ≤ 3 D. m ≤ 3
Đọc tiếp
Tìm tất cả các giá trị của m để hàm số y = x 3 3 – ( m - 1 ) x 2 + 2 ( m - 1 ) x + 2 đồng biến trên tập xác định của nó là:
A. 1 < m < 3
B. m ≥ 1
C. 1 ≤ m ≤ 3
D. m ≤ 3
Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\sqrt{x-m}-\sqrt{6-2x}\)
có tập xác định là 1 đoạn trên trục số là
\(\left\{{}\begin{matrix}m\le x\\x\le3\end{matrix}\right.\Rightarrow m\le3\Rightarrow\left[m;3\right]\)
Vay \(m\le3\) thi ham so co tap xd la 1 doan tren truc so
P/s: Ve cai truc so ra la hieu
Đúng 1
Bình luận (0)
Tìm tất cả các giá trị của m để hàm s\(\sqrt{x^2+4x-8+m}\)ố y = xác định trên [ 0;8 ]
Hàm xác định trên \(\left[0;8\right]\) khi và chỉ khi với mọi \(x\in\left[0;8\right]\) ta có:
\(x^2+4x-8+m\ge0\)
\(\Leftrightarrow m\ge-x^2-4x+8\)
\(\Leftrightarrow m\ge\max\limits_{\left[0;8\right]}\left(-x^2-4x+8\right)\)
Xét hàm \(f\left(x\right)=-x^2-4x+8\) trên \(\left[0;8\right]\)
\(-\dfrac{b}{2a}=-2< 0\Rightarrow\) hàm nghịch biến trên \(\left[0;8\right]\)
\(\Rightarrow\max\limits_{\left[0;8\right]}f\left(x\right)=f\left(0\right)=8\)
\(\Rightarrow m\ge8\)
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để hàm số
y
x
+
2
-
m
x
+
1
nghịch biến trên các khoảng mà nó xác định? A.
m
≤
1
....
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = x + 2 - m x + 1 nghịch biến trên các khoảng mà nó xác định?
A. m ≤ 1 .
B.m<1
C.m<-3
D. m ≤ - 3 .