Giải thích giúp em câu 2 với ạ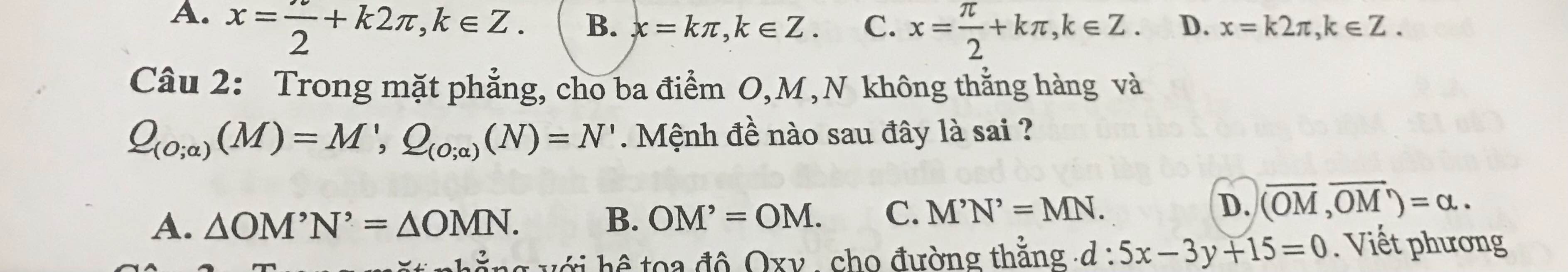

Những câu hỏi liên quan
Mọi người giải giúp em 2 câu này với ạ
3 tạ15 kg=.....................kg
Điền dấu >,<,=vào chỗ chấm sao cho thích hợp
4,3...............4,27
giải giúp em với ạ
Mọi người giải giúp em 2 câu này với ạ
3 tạ15 kg=..........315...........kg
Điền dấu >,<,=vào chỗ chấm sao cho thích hợp
4,3.......>........4,27
Đúng 4
Bình luận (3)
Xem thêm câu trả lời
Giúp em câu 2 với ạ( giải thích tại sao lại là đáp án đó)
hilly nhé
ở đây ta dùng tính từ do đứng trc danh từ
Đúng 3
Bình luận (0)
Giải gấp giúp em với. Giải từng câu và giải thích nhé ạ. Em cảm ơn
Đọc tiếp




 Giải gấp giúp em với. Giải từng câu và giải thích nhé ạ. Em cảm ơn
Giải gấp giúp em với. Giải từng câu và giải thích nhé ạ. Em cảm ơn
Mn giúp em giải và giải thích từng câu với ạ!

\(y=\dfrac{sinx+2cosx+1}{sinx+cosx+2}\)
Thấy : \(sinx+cosx+2\ge-1-1+2=0\) . " = " ko xảy ra nên : \(sinx+cosx+2>0\)
Suy ra : \(\left(y-1\right)sinx+\left(y-2\right)cosx=1-2y\) (*)
(*) có no \(\Leftrightarrow\left(y-1\right)^2+\left(y-2\right)^2\ge\left(1-2y\right)^2\Leftrightarrow2y^2-6y+5\ge4y^2-4y+1\Leftrightarrow-2y^2-2y+4\ge0\)
\(\Leftrightarrow-y^2-y+2\ge0\) \(\Leftrightarrow-2\le y\le1\)
Suy ra : Max y = 1 . Chọn B
Đúng 1
Bình luận (0)
21 : \(cosx-\sqrt{3}sinx=0\)
cos x = 0 thay vào : sin x = 0 ( L )
cos x khác 0 \(\Leftrightarrow x\ne\dfrac{\pi}{2}+k\pi\left(k\in Z\right)\); ta có : \(1-\sqrt{3}tanx=0\Leftrightarrow tanx=\dfrac{1}{\sqrt{3}}\Leftrightarrow x=\dfrac{\pi}{6}+k\pi\left(k\in Z\right)\)
Đúng 0
Bình luận (0)
Mn giúp em giải và giải thích từng câu với ạ
49.
\(\Leftrightarrow m.sin2x+2\left(cos2x+1\right)=m+5\)
\(\Leftrightarrow m.sin2x+2cos2x=m+3\)
Pt có nghiệm khi:
\(m^2+2^2\ge\left(m+3\right)^2\)
\(\Leftrightarrow6m\le-5\Rightarrow m\le-\dfrac{5}{6}\)
\(\Rightarrow m=\left\{-3;-2;-1\right\}\)
50.
\(\Leftrightarrow m.2sin^2x+4sinx.cosx+3m.2cos^2x=2\)
\(\Leftrightarrow m\left(1-cos2x\right)+2sin2x+3m\left(1+cos2x\right)=2\)
\(\Leftrightarrow m.cos2x+sin2x=1-2m\)
Pt có nghiệm khi:
\(m^2+1\ge\left(1-2m\right)^2\Leftrightarrow3m^2-4m\le0\)
\(\Rightarrow m\in\left[0;\dfrac{4}{3}\right]\)
Đúng 0
Bình luận (0)
51.
ĐKXĐ: \(x\ne k\pi\)
\(\dfrac{5-4cosx}{sinx}=\dfrac{6tana}{1+tan^2a}\)
\(\Leftrightarrow\dfrac{5-4cosx}{sinx}=\dfrac{6sina}{cosa}.cos^2a=3sin2a\)
\(\Leftrightarrow5-4cosx=3sin2a.sinx\)
\(\Leftrightarrow3sin2a.sinx+4cosx=5\)
Pt có nghiệm khi:
\(\left(3sin2a\right)^2+4^2\ge5^2\)
\(\Leftrightarrow sin^22a\ge1\)
\(\Leftrightarrow sin^22a=1\Leftrightarrow cos2a=0\)
\(\Leftrightarrow2a=\dfrac{\pi}{2}+k\pi\Rightarrow a=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
\(\Rightarrow a=\left\{\dfrac{\pi}{4};\dfrac{3\pi}{4};\dfrac{5\pi}{4};\dfrac{7\pi}{4}\right\}\)
Em tự cộng và chọn kết quả nhé
Đúng 0
Bình luận (0)
52.
\(\Leftrightarrow2sin\left(2x+\dfrac{\pi}{6}\right)+2sin\left(\dfrac{\pi}{2}\right)=m^2+\sqrt{3}sin2x-cos2x\)
\(\Leftrightarrow2sin2x.cos\left(\dfrac{\pi}{6}\right)+2cos2x.sin\left(\dfrac{\pi}{6}\right)+2=m^2+\sqrt{3}sin2x-cos2x\)
\(\Leftrightarrow\sqrt{3}sin2x+cos2x+2=m^2+\sqrt{3}sin2x-cos2x\)
\(\Leftrightarrow2cos2x=m^2-2\)
\(\Leftrightarrow cos2x=\dfrac{m^2-2}{2}\)
Do \(-1\le cos2x\le1\) nên pt có nghiệm khi:
\(-1\le\dfrac{m^2-2}{2}\le1\Leftrightarrow0\le m^2\le4\)
\(\Leftrightarrow m\in\left[-2;2\right]\)
\(\Rightarrow a+b=0\)
Đúng 0
Bình luận (0)
Mn giúp em giải và giải thích từng câu với ạ
13.
\(y=1+sin2x-\left(1-sin^22x\right)=sin^22x+sin2x\)
\(y=\left(sin2x+\dfrac{1}{2}\right)^2-\dfrac{1}{4}\ge-\dfrac{1}{4}\)
\(\left\{{}\begin{matrix}sin^22x\le1\\sin2x\le1\end{matrix}\right.\) \(\Rightarrow y\le1+1=2\)
\(\Rightarrow\left\{{}\begin{matrix}a=-\dfrac{1}{4}\\b=2\end{matrix}\right.\)
\(\Rightarrow4a+b=1\)
14.
\(\Leftrightarrow\left[{}\begin{matrix}2x-\dfrac{\pi}{4}=x+\dfrac{3\pi}{4}+k2\pi\\2x-\dfrac{\pi}{4}=\dfrac{\pi}{4}-x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\pi+k2\pi\\x=\dfrac{\pi}{6}+\dfrac{k2\pi}{3}\end{matrix}\right.\)
\(\Rightarrow x=\left\{\dfrac{\pi}{6};\dfrac{5\pi}{6}\right\}\)
\(\Rightarrow\dfrac{\pi}{6}+\dfrac{5\pi}{6}=\pi\)
Đúng 0
Bình luận (0)
15.
\(3cosx+2cos^2x-1-cos3x+1=cosx-cos3x\)
\(\Leftrightarrow cos^2x+cosx=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\cosx=-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=\pi+k2\pi\end{matrix}\right.\)
\(\Rightarrow\) Nghiệm lớn nhất \(x=\dfrac{3\pi}{2}\)
\(sin\left(\dfrac{3\pi}{2}-\dfrac{\pi}{4}\right)=-\dfrac{\sqrt{2}}{2}\)
16.
\(cos\left(2x+\dfrac{2\pi}{3}\right)+4cos\left(\dfrac{\pi}{6}-x\right)=\dfrac{5}{2}\)
\(\Leftrightarrow cos\left[\pi-2\left(\dfrac{\pi}{6}-x\right)\right]+4cos\left(\dfrac{\pi}{6}-x\right)=\dfrac{5}{2}\)
\(\Leftrightarrow-cos\left[2\left(\dfrac{\pi}{6}-x\right)\right]+4cos\left(\dfrac{\pi}{6}-x\right)=\dfrac{5}{2}\)
\(\Leftrightarrow1-2cos^2\left(\dfrac{\pi}{6}-x\right)+4cos\left(\dfrac{\pi}{6}-x\right)=\dfrac{5}{2}\)
\(\Leftrightarrow1-2t^2+4t=\dfrac{5}{2}\Leftrightarrow4t^2-8t+3=0\)
Đúng 0
Bình luận (1)
Mn giúp em giải và giải thích từng câu với ạ

17.
\(sin2x=sinx\Rightarrow\left\{{}\begin{matrix}2x=x+k2\pi\\2x=\pi-x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=k2\pi\\x=\dfrac{\pi}{3}+\dfrac{k2\pi}{3}\end{matrix}\right.\)
Nghiệm dương nhỏ nhất: \(x=\dfrac{\pi}{3}\)
18.
\(-1\le sin3x\le1\Rightarrow-1\le y\le4\)
\(miny=-1\) ; \(maxy=4\)
Đúng 2
Bình luận (0)
18 ver 1
Câu này trắc nghiệm điển hình, chỉ thay \(x=40^0\) vào 4 đáp án để thử, ko ai tự luận nó cả
19.
ĐKXĐ:
\(cos\left(2x-\dfrac{\pi}{3}\right)\ne0\)
\(\Leftrightarrow2x-\dfrac{\pi}{3}\ne\dfrac{\pi}{2}+k\pi\)
\(\Leftrightarrow x\ne\dfrac{5\pi}{12}+\dfrac{k\pi}{2}\)
Đúng 2
Bình luận (0)
Mn giúp em giải và giải thích từng câu với ạ
27.
\(cos\left(\dfrac{x}{2}+15^0\right)=sinx\)
\(\Leftrightarrow cos\left(\dfrac{x}{2}+15^0\right)=cos\left(90^0-x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{x}{2}+15^0=90^0-x+k360^0\\\dfrac{x}{2}+15^0=x-90^0+k360^0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=50^0+k240^0\\x=210^0+k720^0\end{matrix}\right.\)
Với \(k=1\Rightarrow x=50^0+240^0=290^0\)
28.
\(sin\left(x-\dfrac{\pi}{4}\right)\ne0\)
\(\Leftrightarrow x-\dfrac{\pi}{4}\ne k\pi\)
\(\Leftrightarrow x\ne\dfrac{\pi}{4}+k\pi\)
Đúng 2
Bình luận (0)
29.
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{3}\right)=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{3}=\dfrac{\pi}{4}+k2\pi\\x+\dfrac{\pi}{3}=-\dfrac{\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{12}+k2\pi\\x=-\dfrac{7\pi}{12}+k2\pi\end{matrix}\right.\)
\(\Rightarrow x=\left\{\dfrac{17\pi}{12};\dfrac{23\pi}{12}\right\}\)
30.
Pt \(2sinx+3cosx=1\) có \(2^2+3^2>1^2\) nên có nghiệm
Đúng 2
Bình luận (0)
31.
Hàm \(y=tan\left(kx\right)\) tuần hoàn với chu kì \(T=\dfrac{\pi}{\left|k\right|}\)
Nên hàm đã cho tuần hoàn với chu kì \(T=\dfrac{\pi}{2}\)
32.
\(sinx\le1\Rightarrow y\le1+2.1=3\)
Dấu "=" xảy ra khi \(sinx=1\)
\(\Leftrightarrow x=\dfrac{\pi}{2}+k2\pi\)
Đúng 2
Bình luận (0)
Mn giúp em giải và giải thích từng câu với ạ

40.
\(\sqrt{3}tanx-1=0\)
\(\Leftrightarrow tanx=\dfrac{1}{\sqrt{3}}\)
\(\Rightarrow x=30^0+k180^0\)
41.
Từ đồ thị ta thấy hàm đồng biến trên \(\left(-\dfrac{\pi}{2};0\right)\) (đồ thị hàm số chỉ có xu hướng đi lên chứ không có đoạn đi xuống trên toàn miền)
42.
\(\Leftrightarrow1-cos2x-2sin2x+2\left(1+cos2x\right)=1\)
\(\Leftrightarrow cos2x-2sin2x=-2\)
43.
\(cos3x=1\Leftrightarrow4cos^3x-3cosx-1=0\)
\(\Leftrightarrow\left(cosx-1\right)\left(2cosx+1\right)^2=0\Leftrightarrow\left[{}\begin{matrix}cosx=1\\cosx=-\dfrac{1}{2}\end{matrix}\right.\)
\(cos2x=-\dfrac{1}{2}\Leftrightarrow2cos^2x-1=-\dfrac{1}{2}\)
\(\Leftrightarrow cos^2x=\dfrac{1}{4}\Rightarrow\left[{}\begin{matrix}cosx=\dfrac{1}{2}\\cosx=-\dfrac{1}{2}\end{matrix}\right.\)
So sánh 2 pt trên ta thấy chúng có nghiệm chung \(cosx=-\dfrac{1}{2}\)
\(\Leftrightarrow x=\pm\dfrac{2\pi}{3}+k2\pi\)
Đúng 0
Bình luận (0)