a, Vật nhiễm điện cùng loại : A,B 

- 2 loại nhiễm loại điện giống nhau tích thì đẩy nhau

b, Vật nhiễm điện khác loại :C,D

- 2 loại nhiễm loại điện khác nhau điện thì hút nhau

Ta có \(\frac{a}{d}=\frac{c}{b}\Rightarrow\frac{b}{d}=\frac{c}{a}=\frac{c+b}{a+d}\)

Vậy C là phương án đúng

Từ: a/b<c/d bạn nhân cả 2 vế Bất đẳng thức (BĐT) với tích (bxd) là 1 số dương , BĐT không đổi chiều.

Sẽ được ad <cb.

Và ngược lại, nếu ad<cd thì chia 2 vế BĐT cho tích  (bxd) là 1 số dương , BĐT không đổi chiều.

Sẽ được a/b < c/d.

giải giúp luôn đi. ko hỉu j hết Đinh Thùy Linh

\(\frac{a}{b}< \frac{c}{d}\)(với b>0 ; d >0 )

\(\Leftrightarrow\frac{ad}{bd}< \frac{cb}{bd}\)

\(\Leftrightarrow\frac{ad}{bd}.bd< \frac{cb}{bd}.bd\)

\(\Leftrightarrow ad< cb\left(đpcm\right)\)

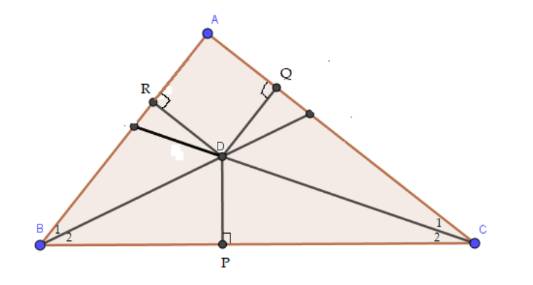
a) Vì BD là tia phân giác của góc ABC nên \(\widehat {{B_1}} = \widehat {{B_2}} = \dfrac{1}{2}.\widehat {ABC}\)

Vì CD là tia phân giác của góc ACB nên \(\widehat {{C_1}} = \widehat {{C_2}} = \dfrac{1}{2}.\widehat {ACB}\)

Xét \(\Delta BDP\) vuông tại P và \(\Delta BDR\) vuông tại R, ta có:

 \(\widehat {{B_2}} = \widehat {{B_1}}\)

BD chung

\( \Rightarrow \Delta BDP = \Delta BDR\) ( cạnh huyền – góc nhọn)

\( \Rightarrow \) DP = DR ( 2 cạnh tương ứng) (1)

b) Xét \(\Delta CDP\) vuông tại P và \(\Delta CDQ\) vuông tại Q, ta có:

 \(\widehat {{C_2}} = \widehat {{C_1}}\)

CD chung

\( \Rightarrow \Delta CDP = \Delta CDQ\) ( cạnh huyền – góc nhọn)

\( \Rightarrow \) DP = DQ ( 2 cạnh tương ứng) (2)

c) Từ (1) và (2), ta được: DR = DQ ( cùng bằng DP).

D nằm trên tia phân giác của góc A do D cách đều AB và AC.

Các vật nhiễm điện dương: a,c,d

Vật nhiễm điện âm: b

Vì các vật có cùng điện tích thì sẽ đẩy nhau. Các vật có điện tích trái dấu sẽ hút nhau.

a hút b => điện tích trái dấu

 b hút c => điện tích trái dấu

c đẩy d  => điện tích cùng dấu

<=>a,c,d là cùng dấu còn b khác dấu

Cách làm đơn giản em có thể a mang điện tích dương (+)

a hút b -> b (-)

b hút c -> c (+)

c đẩy d -> d (+)

Vậy a,c,d cùng dấu, b khác dấu.

a) Ta có:  \(\overrightarrow {AB}  = (3 - 1;4 - 2) = (2;2)\) và \(\overrightarrow {CD}  = (6 - ( - 1);5 - ( - 2)) = (7;7)\)

b) Dễ thấy: \((2;2) = \frac{2}{7}.(7;7)\)\( \Rightarrow \overrightarrow {AB}  = \frac{2}{7}.\overrightarrow {CD} \)

Vậy hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) cùng phương.

c) Ta có: \(\overrightarrow {AC}  = ( - 1 - 1; - 2 - 2) = ( - 2; - 4)\) và \(\overrightarrow {BE}  = (a - 3;1 - 4) = (a - 3; - 3)\)

Để \(\overrightarrow {AC} \) và \(\overrightarrow {BE} \) cùng phương thì \(\frac{{a - 3}}{{ - 2}} = \frac{{ - 3}}{{ - 4}}\)\( \Leftrightarrow a - 3 =  - \frac{3}{2}\)\( \Leftrightarrow a = \frac{3}{2}\)

Vậy \(a = \frac{3}{2}\) hay \(E\left( {\frac{3}{2};1} \right)\) thì hai vectơ \(\overrightarrow {AC} \) và \(\overrightarrow {BE} \) cùng phương

d)

Cách 1:

Ta có: \(\overrightarrow {BE}  = \left( {\frac{3}{2} - 3; - 3} \right) = \left( { - \frac{3}{2}; - 3} \right)\) ; \(\overrightarrow {AC}  = ( - 2; - 4)\)

\( \Rightarrow \overrightarrow {BE}  = \frac{3}{4}.\overrightarrow {AC} \)

Mà \(\overrightarrow {AE}  = \overrightarrow {AB}  + \overrightarrow {BE} \) (quy tắc cộng)

\( \Rightarrow \overrightarrow {AE}  = \overrightarrow {AB}  + \frac{3}{4}.\overrightarrow {AC} \)

Cách 2:

Giả sử \(\overrightarrow {AE}  = m\,.\,\overrightarrow {AB}  + n\,.\,\overrightarrow {AC} \)(*)

Ta có:  \(\overrightarrow {AE}  = \left( {\frac{1}{2}; - 1} \right)\), \(m\,.\,\overrightarrow {AB}  = m\left( {2;2} \right) = (2m;2m)\), \(n\,.\,\overrightarrow {AC}  = n( - 2; - 4) = ( - 2n; - 4n)\)

Do đó (*) \( \Leftrightarrow \left( {\frac{1}{2}; - 1} \right) = (2m;2m) + ( - 2n; - 4n)\)

\(\begin{array}{l} \Leftrightarrow \left( {\frac{1}{2}; - 1} \right) = (2m - 2n;2m - 4n)\\ \Leftrightarrow \left\{ \begin{array}{l}\frac{1}{2} = 2m - 2n\\ - 1 = 2m - 4n\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = 1\\n = \frac{3}{4}\end{array} \right.\end{array}\)

Vậy \(\overrightarrow {AE}  = \overrightarrow {AB}  + \frac{3}{4}.\overrightarrow {AC} \)

Chọn A

A nhé

A