Xét tính đơn điệu, cực trị, giá trị nhỏ nhất, lớn nhất của hàm số:
y=3-3sinx +2cos2x
Những câu hỏi liên quan
22 giờ trước (20:46)
Xét tính đơn điệu, cực trị, giá trị nhỏ nhất, lớn nhất của hàm số:
y=3-3sinx +2cos2x
Hàm tuần hoàn chu kì \(T=2\pi\) nên ta chỉ cần khảo sát trên đoạn \(\left[0;2\pi\right]\)
\(y'=-3cosx-4sin2x=0\Leftrightarrow-cosx\left(3+8sinx\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+k\pi\\x=arcsin\left(-\frac{3}{8}\right)+k2\pi\\x=\pi-arcsin\left(-\frac{3}{8}\right)+k2\pi\end{matrix}\right.\)
Để ngắn gọn thì đặt \(b=2\pi+arcsin\left(-\frac{3}{8}\right)\) ; \(a=\pi-arcsin\left(-\frac{3}{8}\right)\)
BBT:
Hàm đạt cực tiểu tại \(x=\frac{\pi}{2}+k\pi\)
Hàm đạt cực đại tại \(\left[{}\begin{matrix}x=arcsin\left(-\frac{3}{8}\right)+k2\pi\\x=\pi-arcsin\left(-\frac{3}{8}\right)+k2\pi\end{matrix}\right.\)
Hàm đồng biến trên các khoảng \(\left(\frac{\pi}{2}+k2\pi;\pi-arcsin\left(-\frac{3}{8}\right)+k2\pi\right)\) và \(\left(\frac{3\pi}{2}+k2\pi;arcsin\left(-\frac{3}{8}\right)+k2\pi\right)\)
Hàm nghịch biến trên các khoảng \(\left(\pi-arcsin\left(-\frac{3}{8}\right)+k2\pi;\frac{3\pi}{2}+k2\pi\right)\) và \(\left(arcsin\left(-\frac{3}{8}\right)+k2\pi;\frac{5\pi}{2}+k2\pi\right)\)
\(y_{max}=\frac{89}{16}\) khi \(sinx=-\frac{3}{8}\)
\(y_{min}=-2\) khi \(sinx=1\)
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số: y 3.(3sinx + 4cosx)2 +4.(3sinx + 4cosx)+ 1
Đọc tiếp
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số: y= 3.(3sinx + 4cosx)2 +4.(3sinx + 4cosx)+ 1
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau
y
3
(
3
sin
x
+
4
cos
x
)
2
+
4
(
3
sin
x
+
4
cos
x
)
+
1
Đọc tiếp
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau y = 3 ( 3 sin x + 4 cos x ) 2 + 4 ( 3 sin x + 4 cos x ) + 1
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau
y
3
(
3
s
i
n
x
+
4
c
o
s
x
)
2
+
4
3
sin
x
+
4
cos
x
+
1
A. min y
1...
Đọc tiếp
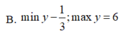
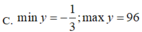
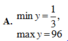
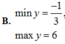
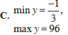
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau y = 3 ( 3 s i n x + 4 c o s x ) 2 + 4 3 sin x + 4 cos x + 1
A. min y = 1 3 ; max y = 96
B. min y = - 1 3 ; max y = 6
C. min y = - 1 3 ; max y = 96
D. min y = 2; max y = 6
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y
2
sin
2
x
+
2
cos
2
x
là: A.
m
i
n
ℝ
y
2
2
;
m...
Đọc tiếp
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2 sin 2 x + 2 cos 2 x là:
A. m i n ℝ y = 2 2 ; m a x ℝ y = 3
B. m i n ℝ y = 2 ; m a x ℝ y = 3
C. m i n ℝ y = 3 ; m a x ℝ y = 3 2
D. m i n ℝ y = 2 ; m a x ℝ y = 3 2
Chọn A.
Ta có: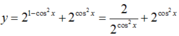 
. Đặt 
, do 0 ≤ cos2x ≤ 1 nên ta có 
Xét hàm số 
có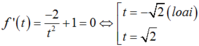 
Lại có 
Vậy 
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
y
3
sin
x
+
4
cos
x
−
1
. A.
max
y
4
,
min
y
−
6
B.
max
y
4
,
min
y
−
3
C.
max
y...
Đọc tiếp
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = 3 sin x + 4 cos x − 1 .
A. max y = 4 , min y = − 6
B. max y = 4 , min y = − 3
C. max y = 2 , min y = − 6
D. max y = 14 , min y = − 6
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = 3sinx+4cosx+1
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y=3sinx+4cosx+1
A. max y=4; min y=-4
B. max y=6; min y=-2
C. max y=6; min y=-4
D. max y=6; min y=-1
Giá trị nhỏ nhất và giá trị lớn nhất của hàm số
y
3
sin
x
+
4
cos
x
+
1
Đọc tiếp
Giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = 3 sin x + 4 cos x + 1
