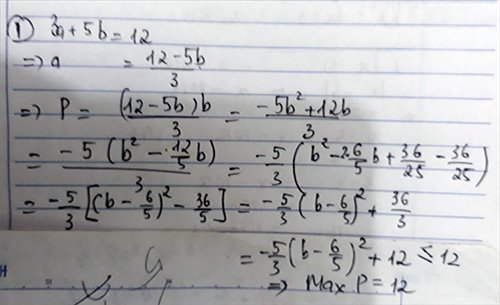tìm min \(\frac{\left(t-1\right)^2+t}{-t}\) t thuộc [-1,1].help

Những câu hỏi liên quan
tìm min \(\left(\frac{\left(t-\frac{1}{2}\right)^2-\frac{5}{4}}{t-2}\right)\)trong khoảng [-1,1]
\(y=\frac{t^2-t-1}{t-2}=\frac{t^2-t-1}{t-2}+\frac{1}{3}-\frac{1}{3}=\frac{3t^2-2t-5}{3\left(t-2\right)}-\frac{1}{3}=\frac{\left(t+1\right)\left(3t-5\right)}{3\left(t-2\right)}-\frac{1}{3}\)
\(=\frac{\left(t+1\right)\left(5-3t\right)}{3\left(2-t\right)}-\frac{1}{3}\ge-\frac{1}{3}\)
\(y_{min}=-\frac{1}{3}\) khi \(t=-1\)
1.tìm max A(frac{x}{x+2020})^2 với x0
2. tìm min C frac{left(4x+1right)left(4+xright)}{x} với x dương
3.cho 3a+5b12. tìmmin Bab
4.tìm min x^2-x+4+frac{1}{x^2-x}
5. cho x,y là 2 số thỏa mãn 2x^2+frac{1}{x^2}+frac{y}{4}4.tìm min max của xy
6. cho a,b0 và a+b1. tìm min Mleft(1+frac{1}{a}right)^2left(1+frac{1}{b}right)^2
Đọc tiếp
1.tìm max A=(\(\frac{x}{x+2020}\))\(^2\) với x>0
2. tìm min C= \(\frac{\left(4x+1\right)\left(4+x\right)}{x}\) với x dương
3.cho 3a+5b=12. tìmmin B=ab
4.tìm min \(x^2-x+4+\frac{1}{x^2-x}\)
5. cho x,y là 2 số thỏa mãn \(2x^2+\frac{1}{x^2}+\frac{y}{4}=4\).tìm min max của xy
6. cho a,b>0 và a+b=1. tìm min M=\(\left(1+\frac{1}{a}\right)^2\left(1+\frac{1}{b}\right)^2\)
Tìm x,y,z,t thuộc Z biết: \(\frac{27}{4}=\frac{-x}{3}=\frac{3}{y^2}=\frac{\left(z+3\right)^2}{-4}=\left|t-2\right|\)
t thuộc N
Cho x,y >0 t/m x+y=1
Tìm min \(M=\left(x^2+\frac{1}{y^2}\right)\left(y^2+\frac{1}{x^2}\right)\)
Trả lời :
Bn tham khảo link này ạ :
Câu hỏi của Cuồng Song Joong Ki - Toán lớp 9 - Học toán với OnlineMath
Bài lm của bn : ★Ƙ - ƔƤČ★ - Trang của ★Ƙ - ƔƤČ★ - Học toán với OnlineMath nhé !
Chúc bn hc tốt <3
( Dô thống kê hỏi đáp sẽ thấy )
Cho các số thực dương x,y,z t/m \(\sqrt{x}+\sqrt{y}+\sqrt{z}=1\)
Tìm Min T \(=\frac{x^2}{y}+\frac{y^2}{z}+\frac{z^2}{x}-\left(x-y\right)^2-\left(y-z\right)^2-\left(z-x\right)^2\)
Cho các số thực dương x,y,z t/m \(\sqrt{x}+\sqrt{y}+\sqrt{z}=1\)
Tìm Min T \(=\frac{x^2}{y}+\frac{y^2}{z}+\frac{z^2}{x}-\left(x-y\right)^2-\left(y-z\right)^2-\left(z-x\right)^2\)
Để lên lớp 9 rồi em giải cho
Mà em thấy CTV đâu rồi nhỉ
Các bn CTV phải giúp đỡ tình trạng thế này nhé
Chúc bn hok giỏi , sớm có người giải cho bn bài này
Đúng 0
Bình luận (0)
Cho các số thực dương x,y,z t/m \(\sqrt{x}+\sqrt{y}+\sqrt{z}=1\) 1
Tìm Min T \(=\frac{x^2}{y}+\frac{y^2}{z}+\frac{z^2}{x}-\left(x-y\right)^2-\left(y-z\right)^2-\left(z-x\right)^2\)
tìm min của t=\(\frac{7\left(a+b\right)^2-9\left(a-b\right)^2}{2014\left(a^2+b^2\right)}\)
Cho x,y>0 t/m x+y=1. Tìm Min P=\(\left(1+\frac{1}{x}\right)\left(1+\frac{1}{y}\right)\)
\(P=\left(1+\frac{1}{x}\right)\left(1+\frac{1}{y}\right)=1+\frac{1}{x}+\frac{1}{y}+\frac{1}{xy}=1+\frac{2}{xy}\ge1+\frac{2}{\frac{\left(x+y\right)^2}{4}}=9\)
Dấu "=" xảy ra <=> x = y = 1/2
Vậy min P = 9 đạt tại x = y = 1/2
\(P=\left(1+\frac{1}{x}\right)\left(1+\frac{1}{y}\right)\)
\(=\left(1+\frac{x+y}{x}\right)\left(1+\frac{x+y}{y}\right)\)
\(=\left(1+1+\frac{y}{x}\right)\left(1+1+\frac{x}{y}\right)\)
\(=4+\frac{2y}{x}+\frac{2x}{y}+1=5+\frac{2y}{x}+\frac{2x}{y}\)
Áp dụng BĐT cô si cho 3 số dương ta được :
\(5+\frac{2y}{x}+\frac{2x}{y}\ge5+2\sqrt{\frac{2y}{x}.\frac{2x}{y}}=9\)
Dấu "=" xảy ra khi \(\frac{2y}{x}=\frac{2x}{y}\Leftrightarrow x^2=y^2\Leftrightarrow x=y=\frac{1}{2}\left(x,y>0;x+y=1\right)\)
Bài này có rất nhiều cách giải,sau đây mình xin liệt kê bốn cách
Cách 1:
\(\left(1+\frac{1}{x}\right)\left(1+\frac{1}{y}\right)=\frac{1}{x}+\frac{1}{y}+\frac{1}{xy}+1\ge\frac{4}{x+y}+\frac{1}{\frac{\left(x+y\right)^2}{4}}+1=9\)
Cách 2:
Theo Cô-si
\(\frac{1}{x}+1=\frac{1}{2x}+\frac{1}{2x}+1\ge3\sqrt[3]{\frac{1}{4x^2}}\) ; \(\frac{1}{y}+1=\frac{1}{2y}+\frac{1}{2y}+1\ge3\sqrt[3]{\frac{1}{4y^2}}\)
\(\Rightarrow\left(1+\frac{1}{x}\right)\left(1+\frac{1}{y}\right)\ge9\sqrt[3]{\frac{1}{16x^2y^2}}\ge9\sqrt[3]{\frac{1}{\left(x+y\right)^4}}=9\)
Cách 3:
Theo Bunhiakvsky
\(\left(1+\frac{1}{x}\right)\left(1+\frac{1}{y}\right)\ge\left(1+\frac{1}{\sqrt{xy}}\right)^2\ge\left(1+\frac{1}{\frac{x+y}{2}}\right)^2=9\)
Cách 4:
Từ điều kiện ta có thể suy ra \(y=1-x\left(0< x< 1\right)\)
Xét
\(\left(1+\frac{1}{x}\right)\left(1+\frac{1}{1-x}\right)-9=\frac{\left(2x-1\right)^2}{\left(1-x\right)x}\ge0\)