Cho C là đồ thị hs y=sinx, C` là đồ thị hàm số y=cos x. Xác định phép tịnh tiến C thành C`
Những câu hỏi liên quan
Tịnh tiến đồ thị hàm số y= cos x sang phải \(\dfrac{\pi}{2}\) ta được đồ thị hàm số nào
A. \(y=sinx\)
B.\(y=-cosx\)
C.\(y=\)\(cos\left(x+\dfrac{\pi}{2}\right)\)
D.\(y=sin\left(x-\dfrac{\pi}{2}\right)\)
Có bao nhiêu phép tịnh tiến biến đồ thị của hàm số
y = sinx thành chính nó?
A. 0
B. 1
C. 2
D. Vô số
Chọn D
Có vô số phép tịnh tiến theo véc tơ k 2 π với k ∈ ℤ
Đúng 0
Bình luận (0)
Giả sử đồ thị của hàm số y f (x) là (C), khi tịnh tiến (C) theo Ox qua phải 1 đơn vị thì sẽ được đồ thị của hàm số:
Đọc tiếp
Giả sử đồ thị của hàm số y = f (x) là (C), khi tịnh tiến (C) theo Ox qua phải 1 đơn vị thì sẽ được đồ thị của hàm số:
Giả sử đồ thị của hàm số y f (x) là (C), khi tịnh tiến (C) theo Oy xuống dưới 1 đơn vị thì sẽ được đồ thị của hàm số:
Đọc tiếp
Giả sử đồ thị của hàm số y = f (x) là (C), khi tịnh tiến (C) theo Oy xuống dưới 1 đơn vị thì sẽ được đồ thị của hàm số:
Đồ thị hàm số ysinx được suy ra từ đồ thị (C) của hàm số ycos x+1 bằng cách A. Tịnh tiến (C) qua trái một đoạn có độ dài là
π
2
và lên trên 1 đơn vị B. Tịnh tiến (C) qua phải một đoạn có độ dài là
π
2
và lên trên 1 đơn vị C. Tịnh tiến (C) qua trái một đoạn có độ dài là
π
2
và xuống dưới 1 đơn vị D. Tịnh tiến (C) qua trái một đoạn...
Đọc tiếp
Đồ thị hàm số y=sinx được suy ra từ đồ thị (C) của hàm số y=cos x+1 bằng cách
A. Tịnh tiến (C) qua trái một đoạn có độ dài là π 2 và lên trên 1 đơn vị
B. Tịnh tiến (C) qua phải một đoạn có độ dài là π 2 và lên trên 1 đơn vị
C. Tịnh tiến (C) qua trái một đoạn có độ dài là π 2 và xuống dưới 1 đơn vị
D. Tịnh tiến (C) qua trái một đoạn có độ dài là π 2 và xuống dưới 1 đơn vị
Tịnh tiến đồ thị hàm số
y
sin
x
sang bên trái
π
2
đơn vị được đồ thị hàm số nào dưới đây? A. Đồ thị hàm số
y
cot
x
B. Đồ thị hàm số
y
cos
x
C. Đồ thị hàm số
y
sin
x
D. Đồ thị hàm số
y
tan
x
Đọc tiếp
Tịnh tiến đồ thị hàm số y = sin x sang bên trái π 2 đơn vị được đồ thị hàm số nào dưới đây?
A. Đồ thị hàm số y = cot x
B. Đồ thị hàm số y = cos x
C. Đồ thị hàm số y = sin x
D. Đồ thị hàm số y = tan x
Giả sử đồ thị của hàm số
y
x
4
-
2
x
2
-
1
là
C
, khi tịnh tiến
C
theo
O
y
lên trên 1 đơn vị thì sẽ được đồ thị của hàm số
Đọc tiếp
Giả sử đồ thị của hàm số y = x 4 - 2 x 2 - 1 là C , khi tịnh tiến C theo O y lên trên 1 đơn vị thì sẽ được đồ thị của hàm số
Chọn A.
Đặt f ( x ) = x 4 - 2 x 2 - 1 thì khi tịnh tiến (C) theo O y lên trên 1 đơn vị thì sẽ được đồ thị của y = f ( x ) + 1 = x 4 - 2 x 2 .
Đúng 0
Bình luận (0)
Xác định phép tịnh tiến để biến đồ thị (H): y= | x+1 | thành (H') : y= |x-1| + 3
Cho hàm số
y
cos
2
x
.a) Chứng minh rằng cos
2
x
+
k
π
cos
2
x
với mọi số nguyên k. Từ đó vẽ đồ thị (C) của hàm số
y
cos
2
x
.b) Viết phương...
Đọc tiếp
Cho hàm số y = cos 2 x .
a) Chứng minh rằng cos 2 x + k π = cos 2 x với mọi số nguyên k. Từ đó vẽ đồ thị (C) của hàm số y = cos 2 x .
b) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ x = π / 3 .
c) Tìm tập xác định của hàm số : z = 1 - cos 2 x 1 + cos 2 2 x
a) + Hàm số y = cos x có chu kì 2π.
Do đó: cos 2.(x + kπ) = cos (2x + k2π) = cos 2x.
⇒ Hàm số y = cos 2x cũng tuần hoàn với chu kì π.
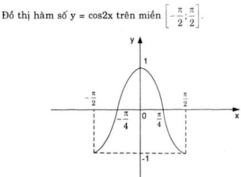
Từ đó suy ra
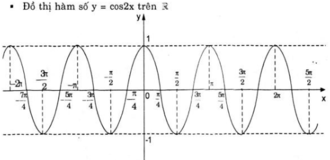
b. y = f(x) = cos 2x
⇒ y’ = f’(x) = (cos 2x)’ = -(2x)’.sin 2x = -2.sin 2x.
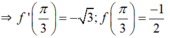
⇒ Phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ x = π/3 là:
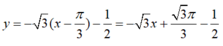
c. Ta có: 1 – cos 2x = 2.sin2x ≥ 0.
Và 1 + cos22x > 0; ∀ x
⇒ 
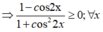
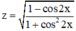luôn xác định với mọi x ∈ R.
Đúng 0
Bình luận (0)