a) Tổng số đo của góc trong và góc ngoài ở mỗi đỉnh của tứ giác (lồi) là 180⁰ Þ Tổng số đo các góc trong và các góc ngoài của tứ giacs là 4.180⁰ = 720⁰.

Mặt khác, tổng số đo các góc trong của tứ giác là: (4-2).180⁰ = 360⁰.

Þ Tổng số đo các góc ngoài của tứ giác là: 720⁰ - 360⁰ = 360⁰

Tương tự, ta cũng tính được tổng số đo các góc ngoài của ngũ giác và thập giác là 360⁰.

b) Tổng số đo của góc trong và góc ngoài ở mỗi đỉnh của hình n - giác (lồi) là 180⁰ Þ Tổng số đo các góc trong và các góc ngoài của đa giác là n.180⁰.

Mặt khác, tổng số đo các góc trong của đa giác là (n - 2).180⁰.

Þ Tổng số đo các góc ngoài của đa giác là:

n.180⁰ - (n - 2).180⁰ = 360⁰.

A:B:C:D=1:2:3:4

\(\frac{A}{1}=\frac{B}{2}=\frac{C}{3}=\frac{D}{4}\) Ap dung tinh chat day ti so bang nhau ta co

\(\frac{A}{1}=\frac{B}{2}=\frac{C}{3}=\frac{D}{4}=A+B+C+D:10=360:10=36\)

=>A=36 ;B=72;C=108;D=144

TINH CAC GOC NGOAI

\(A_2+B_2+C_2+D_2=\left(180-36\right)+\left(180-72\right)+\left(180-108\right)+\left(180-144\right)\)

\(A_2+B_2+C_2+D_2=720-360=360\)

1 ta có :1 tứ giác có 4 góc và tổng phải bằng 360 độ mà 4 góc nhọn sẽ bé hơn 360(vì 1 góc nhọn <90 độ ) nên cac góc ko thể đều là góc nhọn.Đối với góc tù vẫn tương tự

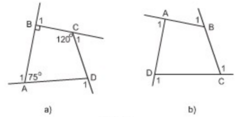
a) + Góc ngoài tại A là góc A1:

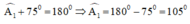
+ Góc ngoài tại B là góc B1:

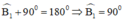
+ Góc ngoài tại C là góc C1:

+ Góc ngoài tại D là góc D1:

Theo định lý tổng các góc trong một tứ giác bằng 360º ta có:

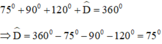
Lại có:

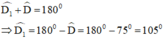
Vậy góc ngoài tại D bằng 105º.

b) Hình 7b:

Ta có:

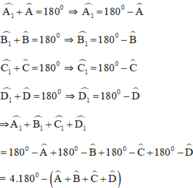
Mà theo định lý tổng bốn góc trong một tứ giác bằng 360º ta có:

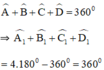
c) Nhận xét: Tổng các góc ngoài của tứ giác cũng bằng 360º.

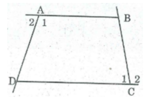
* Gọi ∠ A 1 ,  ∠ C 1 là góc trong của tứ giác tại đỉnh A và C,  ∠ A 2 ,  ∠ C 2 là góc ngoài tại đỉnh A và C.

Ta có:  ∠ A 1 +  ∠ A 2  = 180 0  (2 góc kề bù)

⇒  ∠ A 2 =  180 0  -  ∠ A 1

∠ C 1 +  ∠ C 2 =  180 0  (2 góc kề bù) ⇒  ∠ C 2 =  180 0  -  ∠ C 1

Suy ra:  ∠ A 2 +  ∠ C 2 =  180 0  -  ∠ A 1 + 180o -  ∠ C 1 =  360 0  – ( ∠ A 1  +  ∠ C 1 ) (1)

* Trong tứ giác ABCD ta có:

∠ A 1 +  ∠ B +  ∠ C 1  + ∠ D =  360 0  (tổng các góc của tứ giác)

⇒  ∠ B +  ∠ D =  360 0  - ( ∠ A 1  +  ∠ C 1 ) (2)

Từ (1) và (2) suy ra:  ∠ A 2 +  ∠ C 2  =  ∠ B +  ∠ D

 Ta có góc B2 = 180 độ - góc B1

 góc C2 = 180 độ - góc C1 

=> góc B2 + góc C2 = 360 độ - ( góc B1 + góc C1 )   (1)

Tứ giác ABCD có góc A + góc B + góc C + góc D = 360 độ 

=>  góc A + góc D = 360 độ - ( góc B1 + góc C1 )   (2) 

Từ (1), (2) => góc B2 + góc C2 = góc A + góc D 

Vậy tổng 2 góc ngoài tại 2 đỉnh bằng tổng 2 góc trong tại các đỉnh còn lại

gọi các góc trong của đỉnh A và C là ^A₁ và ^C₁

còn các góc ngoài của đỉnh A và C là ^A₂ và ^C₂

ta có ^A1 + ^A2 =180^o ( 2 góc kè bù )

và ^C1 +^C2 =180^o (2 góc kề bù )

=> ^A2 =180^o -^A1

và ^C2 =180^o -^C2

=> ^A2+^C2 = 360^o -^A1-^C1(1)

ta lại có ^A1+^B+^C1+^D =360^o (tổng 4 góc tứ giác )

=> ^B+^D = 360^o - ^A1-^C1(2)

từ (1) và(2) => ^B+^D = ^A2 +^C2 (cùng = 360⁰ -^a1 -^C1)

vậy.............

Gọi \(\widehat{A_1},\widehat{C_1}\) là góc trong của tứ giác tại đỉnh A và C. \(\widehat{A_1}=\widehat{C}_1\) là góc ngoài tại đỉnh A và C.

Ta có: \(\widehat{A_1}+\widehat{A_2}=180^0\) (2 góc kề bù)

\(\widehat{C_1}+\widehat{C_2}=180^0\)(2 góc kề bù)

Suy ra:

\(\widehat{A_2}+\widehat{C_2}=180^0-\widehat{A_1}+180^0-\widehat{C_1}\)

\(=360^0-\left(\widehat{A_1}+\widehat{C_1}\right)\) (1)

Trong tứ giác ABCD ta có:

\(\widehat{A}+\widehat{B}+\widehat{C_1}+\widehat{D}=360^0\) (tổng các góc của tứ giác)

(2)

Từ (1) và (2) suy ra: \(\widehat{A_1}+\widehat{C_1}=\widehat{B}+\widehat{D}\)