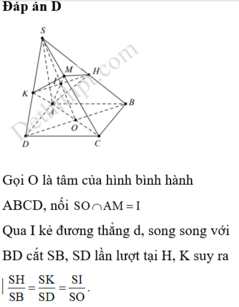
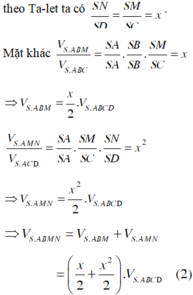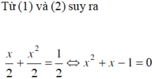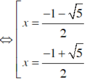Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Mp(α) qua AB và cắt cạnh SC tại
M, cắt cạnh SD tại N sao cho \(\frac{SM}{MC}=\frac{SN}{ND}\) . Mệnh đề nào sau đây là đúng?
A. MN//CD
B. MN cắt BC
C. MN cắt CD
D. MN // SA

Những câu hỏi liên quan
Cho hình chóp có đáy ABCD la hình thang đáy lớn là CD. M là trung điểm của SA, N là giao
điểm của cạnh SB và mp(MCD). Mệnh đề nào sau đây là mệnh đề đúng ?
A. MN và SD cắt nhau B. MN // CD
C. MN và SC cắt nhau D. MN và CD chéo nhau
giải thích các bước
Cho hình chóp S.ABCD, đáy ABCD là hình bình hành, mặt phẳng
α
đi qua AB cắt cạnh SC, SD lần lượt tại M, N. Tính tỉ số
S
N
S
D
để
α
chia khối chóp S.ABCD thành hai phần có thể tích bằng nhau. A.
1
2
B. ...
Đọc tiếp
Cho hình chóp S.ABCD, đáy ABCD là hình bình hành, mặt phẳng α đi qua AB cắt cạnh SC, SD lần lượt tại M, N. Tính tỉ số S N S D để α chia khối chóp S.ABCD thành hai phần có thể tích bằng nhau.
A. 1 2
B. 1 3
C. 5 - 1 2
D. 3 - 1 2
Chọn C

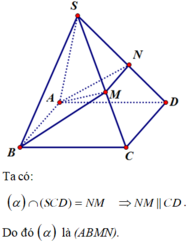
Ta có: α ∩ ( S C D ) = M N ⇒ M N / / C D .
Do đó α là (ABMN).
Mặt phẳng α chia khối chóp thành 2 phần có thể tích bằng nhau là
V S . A B M N = V A B C D M N ⇒ V S . A B M N = 1 2 . V S . A B C D 1
Ta có:
V S . A B C = V S . A C D = 1 2 V S . A B C D
Đặt S N S D = x với (0<x<1), khi đó theo Ta-let ta có S N S D = S M S C = x .
Mặt khác
V S . A B M V S . A B C = S A S A . S B S B . S M S C = x ⇒ V S . A B M = x 2 V S . A B C D
V S . A M N V S . A C D = S A S A . S M S C . S N S D = x 2 ⇒ V S . A M N = x 2 2 V S . A B C D
⇒ V S . A B M N = V S . A B M + V S . A M N = ( x 2 + x 2 2 ) . V S . A B C D 2
Từ (1), (2) suy ra
x 2 + x 2 2 = 1 2 ⇔ x 2 + x - 1 = 0
x = - 1 - 5 2 v à x = - 1 + 5 2
Đối chiếu điều kiện của x ta được S N S D = - 1 + 5 2
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD, đáy ABCD là hình bình hành, mặt phẳng
α
đi qua AB cắt cạnh SC, SD lần lượt tại M, N. Tính tỉ số
S
N
S
D
để
α
chia khối chóp S.ABCD thành hai phần có thể tích bằng nhau. A.
1
2
B.
1
3
C.
5...
Đọc tiếp
Cho hình chóp S.ABCD, đáy ABCD là hình bình hành, mặt phẳng α đi qua AB cắt cạnh SC, SD lần lượt tại M, N. Tính tỉ số S N S D để α chia khối chóp S.ABCD thành hai phần có thể tích bằng nhau.
A. 1 2
B. 1 3
C. 5 - 1 2
D. 3 - 1 2
Cho hình chóp S.ABCD có đáy là hình thang ABCD với AD//BC và AD = 2BC. Gọi M là điểm trên cạnh SD thỏa mãn SM = 1/3SD. Mặt phẳng (ABM) cắt cạnh SC tại N. Tính SN/ SC
Vẫn dùng kĩ thuật cũ:
\(\overrightarrow{AD}-2\overrightarrow{BC}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{AS}+\overrightarrow{SD}-2\overrightarrow{BS}-2\overrightarrow{SC}=0\)
\(\Leftrightarrow\overrightarrow{SA}=2\overrightarrow{SB}-2\overrightarrow{SC}+\overrightarrow{SD}\) (1)
Đặt \(\overrightarrow{SC}=x.\overrightarrow{SN}\)
Giả thiết suy ra \(\overrightarrow{SD}=3\overrightarrow{SM}\)
Thế vào (1): \(\overrightarrow{SA}=2\overrightarrow{SB}-2x.\overrightarrow{SN}+3\overrightarrow{SM}\)
Do A, B, N, M đồng phẳng
\(\Rightarrow2-2x+3=1\)
\(\Rightarrow x=2\Rightarrow SC=2SN\Rightarrow SN=\dfrac{1}{2}SC\)
Đúng 2
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của SA, N là điểm trên đoạn SB sao cho
S
N
2
N
B
.
Mặt phẳng chứa MN cắt đoạn SD tại Q và cắt đoạn SC tại P. Tỉ số
V
S
.
M
N
P
Q
V
S...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của SA, N là điểm trên đoạn SB sao cho S N = 2 N B . Mặt phẳng chứa MN cắt đoạn SD tại Q và cắt đoạn SC tại P. Tỉ số V S . M N P Q V S . A B C D lớn nhất bằng
A. 2/5
B. 1/3
C. 1/4
D. 3/8
Đáp án B
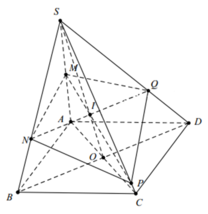
Ta có: V S . M N P V S . A B C = 2 V S . M N P V S . A B C = S M S A . S N S B . S P S C = 1 3 . S P S C
Tương tự V S . M P Q V S . A C D = 2 V S . M P Q V S . A B C D = 1 2 . S P S C . S Q S D
Do đó 2 V S . M N P Q V S . A B C D = 1 3 S P S C + 1 2 . S P S C . S Q S D
Đặt S P S C = x 0 < x ≤ 1 , ta chứng minh được S A S M + S C S P = S B S N + S D S Q = 2 S O S I
Do đó S D S Q = 1 x + 1 2 ⇒ 2 k = x 1 3 + x x + 2 = 2 3
Do 0 < x ≤ 1 nên 2 k m ax = f 1 = 2 3 ⇒ k = 1 3 .
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình thang , AD là đáy lớn . Mặt phẳng (alpha) chứa đường thẳng AB và cắt cạnh SC,SD lần lượt tại các điểm phân biệt M,N ((alpha) # (ABCD)) . Tìm mệnh đề đúng
Xem chi tiết
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là điểm trên cạnh SC sao cho 5SM2SC mặt phẳng
(
α
)
qua A, M và song song với đường thẳng BD cắt hai cạnh SB, SD lần lượt tại H, K. Tính tỉ số thể tích ? A.
1
5
B.
8
35
C.
1
7
D.
6
35
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là điểm trên cạnh SC sao cho 5SM=2SC mặt phẳng ( α ) qua A, M và song song với đường thẳng BD cắt hai cạnh SB, SD lần lượt tại H, K. Tính tỉ số thể tích
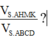 ?
?
A. 1 5
B. 8 35
C. 1 7
D. 6 35
Cho hình chóp
S
.
A
B
C
D
có đáy ABCD là hình bình hành. Gọi M là điểm trên cạnh SC sao cho
5
S
M
2
S
C
,
mặt phẳng
α
qua A, M và song song với đường thẳng BD cắt hai cạnh SB, SD lần lượt tại H, K. Tính tỉ số thể tích
V
S
.
A...
Đọc tiếp
Cho hình chóp S . A B C D có đáy ABCD là hình bình hành. Gọi M là điểm trên cạnh SC sao cho 5 S M = 2 S C , mặt phẳng α qua A, M và song song với đường thẳng BD cắt hai cạnh SB, SD lần lượt tại H, K. Tính tỉ số thể tích V S . A H M K V S . A B C D
A. 1 5
B. 8 35
C. 1 7
D. 6 35
Đáp án D

Gọi O là tâm của hình bình hành ABCD, nối S O ∩ A M = I
Qua I kẻ đương thẳng d, song song với BD cắt SB, SD lần lượt tại H, K suy ra S H S B = S K S D = S I S O .
Điểm M ∈ S C thỏa mãn 5 S M = 2 S C ⇒ S M S C = 2 5
Xét tam giác SAC, có:
M S M C . A C A O . I O I S = 1 ⇒ I O S I = 4 3 ⇒ S I S O = 3 7
Khi đó:
V S . A K M V S . A D C = S K S D . S M S C ; V S . A H M V S . A B C = S H S B . S M S C
Suy ra:
V S . A H M K V S . A B C D = S M S C . S H S B = 2 5 . 3 7 = 6 35 ⇒ V S . A H M K = 6 36 V S . A B C D
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là điểm trên cạnh SC sao cho 5SM2SC mặt phẳng
(
α
)
qua A, M và song song với đường thẳng BD cắt hai cạnh SB, SD lần lượt tại H, K. Tính tỉ số thể tích
V
S
.
A
H
M
K
V
S...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là điểm trên cạnh SC sao cho 5SM=2SC mặt phẳng ( α ) qua A, M và song song với đường thẳng BD cắt hai cạnh SB, SD lần lượt tại H, K. Tính tỉ số thể tích V S . A H M K V S . A B C D ?
A. 1 5
B. 8 35
C. 1 5
D. 6 35