Tìm tất cả các giá trị tham số m để hàm số sau chỉ nhận giá trị dương:
y=(3sinx - 4cosx)2 - 3sinx + 4cosx + m
Những câu hỏi liên quan
Tìm tất cả các giá trị của tham số m để hàm số sau chỉ nhận giá trị dương : y (3sinx - 4cosx)2 - 6sinx + 8cosx + 2m - 1 A. m 1 B. m 1 C. m 2 D. m 1
Đọc tiếp
Tìm tất cả các giá trị của tham số m để hàm số sau chỉ nhận giá trị dương :
y = (3sinx - 4cosx)2 - 6sinx + 8cosx + 2m - 1
A. m = 1
B. m > 1
C. m > 2
D. m < 1
Đáp án B
Đặt t = 3sin x - 4 cos x => -5 ≤ t ≤ 5
Ta có: y = t2 – 2t + 2m – 1 = (t – 1)2 + 2m - 2
Với mọi t ta có (t – 1)2 ≥ 0 nên y ≥ 2m - 2 => min y = 2m - 2
Hàm số chỉ nhận giá trị dương ⇔ y > 0 ∀x ∈ R ⇔ min y > 0
⇔ 2m - 2 > 0 ⇔ m > 1
Đúng 0
Bình luận (0)
27 tháng 12 2022 lúc 12:40
Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\sqrt{8cosx-6sinx-\left(3sinx-4cosx\right)^2-2m}\) có tập xác định là R
Hàm xác định trên R khi và chỉ khi:
\(8cosx-6sinx-\left(3sinx-4cosx\right)^2-2m\ge0;\forall x\) (1)
Đặt \(3sinx-4cosx=t\)
\(\Rightarrow t^2=\left(3sinx-4cosx\right)^2\le\left(3^2+\left(-4\right)^2\right)\left(sin^2x+cos^2x\right)=25\)
\(\Rightarrow-5\le t\le5\)
(1) tương đương:
\(-2t-t^2-2m\ge0;\forall t\in\left[-5;5\right]\)
\(\Leftrightarrow2m\le-t^2-2t;\forall t\in\left[-5;5\right]\)
\(\Leftrightarrow2m\le\min\limits_{t\in\left[-5;5\right]}\left(-t^2-2t\right)\)
Xét hàm \(f\left(t\right)=-t^2-2t\) trên \(\left[-5;5\right]\)
\(-\dfrac{b}{2a}=-1\) ; \(f\left(-5\right)=-15\) ; \(f\left(-1\right)=1\) ; \(f\left(5\right)=-35\)
\(\Rightarrow2m\le-35\Rightarrow m\le-\dfrac{35}{2}\)
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau
y
3
(
3
sin
x
+
4
cos
x
)
2
+
4
(
3
sin
x
+
4
cos
x
)
+
1
Đọc tiếp
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau y = 3 ( 3 sin x + 4 cos x ) 2 + 4 ( 3 sin x + 4 cos x ) + 1
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số: y 3.(3sinx + 4cosx)2 +4.(3sinx + 4cosx)+ 1
Đọc tiếp
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số: y= 3.(3sinx + 4cosx)2 +4.(3sinx + 4cosx)+ 1
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau
y
3
(
3
s
i
n
x
+
4
c
o
s
x
)
2
+
4
3
sin
x
+
4
cos
x
+
1
A. min y
1...
Đọc tiếp
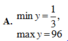
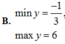
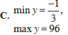
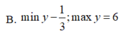
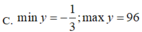
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau y = 3 ( 3 s i n x + 4 c o s x ) 2 + 4 3 sin x + 4 cos x + 1
A. min y = 1 3 ; max y = 96
B. min y = - 1 3 ; max y = 6
C. min y = - 1 3 ; max y = 96
D. min y = 2; max y = 6
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau
y
3
sin
x
+
4
cos
x
+
1
A.
m
i
n
y
-
6
,
m
a
x
y
4
B.
m
i
n
y
-
6
,
m
a
x
y
5
C.
m...
Đọc tiếp
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau y = 3 sin x + 4 cos x + 1
A. m i n y = - 6 , m a x y = 4
B. m i n y = - 6 , m a x y = 5
C. m i n y = - 4 , m a x y = 6
D. m i n y = - 3 , m a x y = 4
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau: y=3sinx+4cosx+1
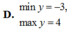
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau y= 3sinx+ 4cosx + 1
A. maxy = 6; min y= - 2
B. max y= 4; min y= -4
C. max y= 6; min y= -4
D. max y= 6; min y= -1
Cho hàm số yf(x) có đồ thị như hình bên dưới.Có bao nhiêu giá trị nguyên của tham số m để phương trình f(3sinx + 4cosx) f(m) có nghiệm? A. 10 B. 14. C. 9 D. 11.
Đọc tiếp
Cho hàm số y=f(x) có đồ thị như hình bên dưới.
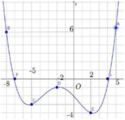
Có bao nhiêu giá trị nguyên của tham số m để phương trình f(3sinx + 4cosx) = f(m) có nghiệm?
A. 10
B. 14.
C. 9
D. 11.
