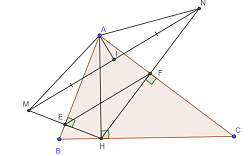
Cho tam giác ABC có đường cao AH .Kẻ HE vuông góc với AB tại E kéo dài HE lấy EM=EH kẻ HF vuông góc với AC tại F , kéo dài HF lấy FN=FH .Gọi I là trung điểm của MN chứng minh rằng
a) AB là trung trực của MH và AC là trung trực của HN
b) tam giác AMN cân
c) EF//MN
d) AI vuông góc EF