Động lượng của vật 1 là:

\(p_1=m_1v_1=5.6=30kg.m/s\)

Động lượng của vật 2 là:

\(p_2=m_2v_2=10.3=30kg.m/s\)

\(a,\) Tổng động lượng của hệ là:

\(p=p_1+p_2=30+30=60kg.m/s\)

Động lượng của hệ cùng phương, cùng chiều với \(\overrightarrow{p_1,}\)\(\overrightarrow{p_2}\)

\(b,\) Tổng động lượng của hệ là:

\(p=p_1-p_2=30-30=0kg.m/s\)

\(c, \) Tổng động lượng của hệ là:

\(p=\sqrt{{p_1}^2+{p_2}^2}=\sqrt{30^2+30^2}=30\sqrt{2}kg.m/s\)

Vì động lượng của vật 1 và vật 2 bằng nhau nên động lượng của hệ hợp \(\overrightarrow{p_1}\), \(\overrightarrow{p_2}\)góc 45 độ.

quãng đường mỗi xe đi trong 1h chênh nhau 10km nên \(v_1-10=v_2\left(1\right)\)

quãng đường xe 1 đi đến C \(v_1.1,5=AC\left(2\right)\)

quãng đường xe 2 đi đến C \(v_2.1,5=BC\) \(\Rightarrow v_2.1,5+AB=AC\) mà AB=1/5AC vì BC+AB=AC mà BC=4AB

\(\Rightarrow v_2.1,5+\dfrac{1}{5}AC=AC\Rightarrow v_2.1,5=\dfrac{4}{5}AC\left(3\right)\)

chia 2 vế 2 3 cho nhau \(\dfrac{v_1}{v_2}=\dfrac{1}{\dfrac{4}{5}}\) kết hợp vs (1) \(\dfrac{v_1}{v_1-10}=\dfrac{1}{\dfrac{4}{5}}\Rightarrow v_1=50\left(km/h\right)\)

=> v2=40(km/h)

=>AC=50.1,5=75(km)

Để mình giúp cho? :D 

a) \(\overrightarrow{v_1}\uparrow\uparrow\overrightarrow{v_2}\) \(\Rightarrow p_h=p_1+p_2=m_1v_1+m_2v_2=6\left(kg.m/s\right)\)

b) \(\overrightarrow{v_1}\uparrow\downarrow\overrightarrow{v_2}\Rightarrow p_h=\left|p_1-p_2\right|=0\left(kg.m/s\right)\)

c) \(\overrightarrow{v_1}\perp\overrightarrow{v_2}\Rightarrow p_h=\sqrt{p_1^2+p_2^2}=\sqrt{\left(m_1v_1\right)^2+\left(m_2v_2\right)^2}=3\sqrt{2}\left(kg.m/s\right)\)

p₁ = m₁v₁ = 1.3 = 3kg.m/s

p₂ = m₂v₂ = 3.1 = 3kg.m/s

a) Động lượng của hệ: = ₁ + ₂ 

Độ lớn của hệ: p = p₁ + p₂ = 3 + 3 = 6kg.m/s

b) Động lượng của hệ: = ₁ + ₂ 

Độ lớn của hệ: p = | p₁ - p₂ | = | 3 - 3 | = 0kg.m/s

c) Động lượng của hệ: = ₁ + ₂ 

Độ lớn của hệ: \(p=\sqrt{p_1^2+p^2_2}=\sqrt{3^2+3^2}=4,242kg.m/s\)

Phân tích: 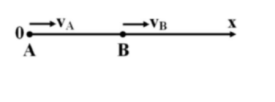                  Cách 1: Từ:  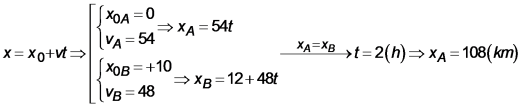  Cách 2: Mỗi giờ xe A đi được nhiều hơn xe B là 54 – 48 = 6km. Muốn xe A đi được nhiều hơn xe B là 12 km thì phải cần thời gian: 12/6 = 2h. Lúc này, xe A đi được: AC = 54.2 = 108 km.

Gấp giùm mk T.T

a). Khi xe II đi về phía A:

V1+V2==

Khi xe II đi ra xa A:

V1-V2=

Lấy (1)+(2), ta được 2V1=16

b. Gọi t là thời gian chuyển động của hai xe

                                                          B1

A                                           A1        B

Xe I đi đoạn AA1:

AA1=V1.t=8t

Suy ra: A1B=700-8t

Xe II đi đoạn BB1:

BB1=V2.t=6t

Xét tam giác A1BB1 vuông tại B có:

A1B1 nhỏ nhất khi:

10t-560=0

t=56 giây

minA1B1==420m

Bài 7 :

- Quãng đường vật đi từ A đến điểm gặp là : \(140v_1\left(m\right)\)

- Quãng đường vật đi từ B đến điểm gặp là : \(140v_2\left(m\right)\)

Mà quãng đường AB dài 420 m

\(\Rightarrow140\left(v_1+v_2\right)=420\)

Mà \(v_2=0,5v_1\)

\(\Rightarrow\left\{{}\begin{matrix}v1=2\\v2=1\end{matrix}\right.\) ( m/s )

Vậy ...

Bài 8 :

- Gọi thời gian hai xe gặp nhau là t ( h, t > 0 )

- Thời gian người đi xe đạp xuất phát trước là : \(\dfrac{16}{v_1}\left(h\right)\)

- Quãng đường từ A đến điểm gặp là : \(S=v.t=\left(t-\dfrac{16}{v1}\right)3v1\left(km\right)\)

Mà quãng đường từ A đến điểm gặp không đổi .

\(\Rightarrow3v_1\left(t-\dfrac{16}{v_1}\right)=16+v_1\left(t-\dfrac{16}{v_1}\right)\)

\(\Rightarrow v_1t=24\)

Vậy quãng đường từ A đến điểm gặp là : \(3v_1t-48=24\left(km\right)\)

Bảo toàn động lượng:

\(\overrightarrow{p_1}+\overrightarrow{p_2}=\overrightarrow{p}\)

Hai vật chuyển động ngược chiều nhau:

\(\Rightarrow-m_1v_1+m_2v_2=\left(m_1+m_2\right)\cdot v\)

\(\Rightarrow v=\dfrac{-2\cdot3+3\cdot5}{2+3}=1,8\)m/s