Đáp án B

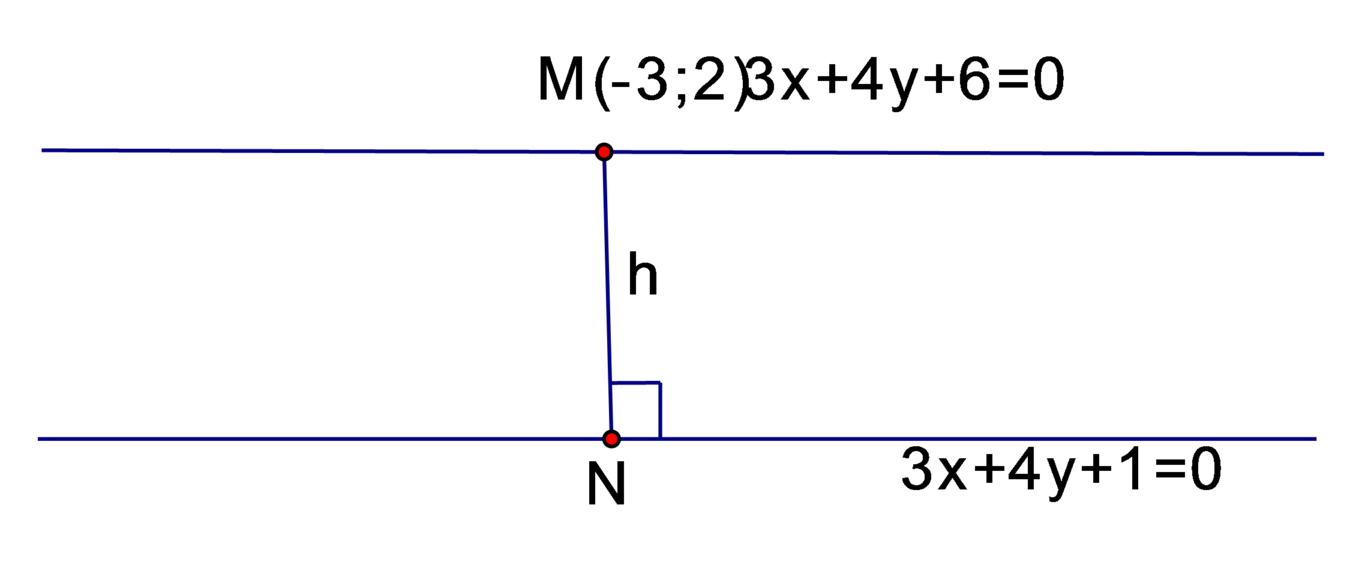
Độ dài véc tơ v →  bé nhất đúng bằng khoảng cách h giữa d và d' . h chính là khoảng cách từ M ∈ d  tới N ∈ d ' sao cho M N → ⊥ u → 4 ; − 3 trong đó u → là VTCP của cả d và d' .Và khi đó:  v → = M N →

Chọn M − 3 ; 2 ∈ d . Ta cần tìm N t ; − 6 − 3 t 4 ∈ d ' sao cho:

M N → t + 3 ; − 14 − 3 t 4 ⊥ u → 4 ; − 3

⇔ 4 t + 12 + 42 + 9 t 4 = 0 ⇔ t = − 18 5

⇒ M N → = − 3 5 ; − 4 5

Đáp án B

Đặt \(\overrightarrow{v}=\left(a;b\right)\Rightarrow a^2+b^2=5\) (1)

Đường thẳng d nhận \(\left(3;-4\right)\) là 1 vtpt nên cũng nhận \(\overrightarrow{u}=\left(4;3\right)\) là 1 vtcp

\(sin\alpha=\dfrac{2}{\sqrt{5}}\Rightarrow cos\alpha=\sqrt{1-sin^2\alpha}=\dfrac{1}{\sqrt{5}}\)

\(\Rightarrow\dfrac{\left|a.4+b.3\right|}{\sqrt{a^2+b^2}.\sqrt{4^2+3^2}}=\dfrac{1}{\sqrt{5}}\Leftrightarrow\left|4a+3b\right|=5\) (2)

Từ (1) và (2) ta được hệ: \(\left\{{}\begin{matrix}a^2+b^2=5\\\left|4a+3b\right|=5\end{matrix}\right.\)

Phá trị tuyệt đối, sử dụng phép thế để giải hệ ta được:

\(\left(a;b\right)=\left(-2;1\right);\left(\dfrac{2}{5};-\dfrac{11}{5}\right);\left(2;-1\right);\left(-\dfrac{2}{5};\dfrac{11}{5}\right)\)

Tổng cộng có 4 vecto \(\overrightarrow{v}\) thỏa mãn 

Tới đây bạn tự làm nốt phần tìm ảnh của d nhé

Gọi d' là đường thẳng qua M và vuông góc d \(\Rightarrow\) d' nhận (4;-3) là 1 vtpt

Phương trình d':

\(4\left(x-2\right)-3\left(y-1\right)=0\Leftrightarrow4x-3y-5=0\)

Gọi N là giao điểm của d và d' \(\Rightarrow\)tọa độ N thỏa mãn:

\(\left\{{}\begin{matrix}3x+4y+10=0\\4x-3y-5=0\end{matrix}\right.\) \(\Rightarrow N\left(-\dfrac{2}{5};-\dfrac{11}{5}\right)\)

M' là ảnh của M qua phép đối xứng trục d \(\Leftrightarrow\) N là trung điểm MM'

\(\Rightarrow\left\{{}\begin{matrix}x_{M'}=2x_N-x_M=-\dfrac{14}{5}\\y_{M'}=2y_N-y_M=-\dfrac{27}{5}\end{matrix}\right.\)

\(\Rightarrow M'\left(-\dfrac{14}{5};-\dfrac{27}{5}\right)\)

Lời giải:
Gọi $M'(a,b)$ là ảnh của $M$ đối xứng qua $d$
$\overrightarrow{MM'}=(a-2,b-1)$

Vì $\overrightarrow{MM'}\perp \overrightarrow{u_d}$ nên:

$\frac{a-2}{2}=\frac{b-1}{1}\Leftrightarrow a-2=2(b-1)(1)$

$I$ là trung điểm $MM'$. $x_I=\frac{2+a}{2}; y_I=\frac{b+1}{2}$

$3.\frac{2+a}{2}+4.\frac{b+1}{2}+10=0$

$\Leftrightarrow 3a+4b+30=0(2)$

Từ $(1);(2)\Rightarrow a=-6;b=-3$