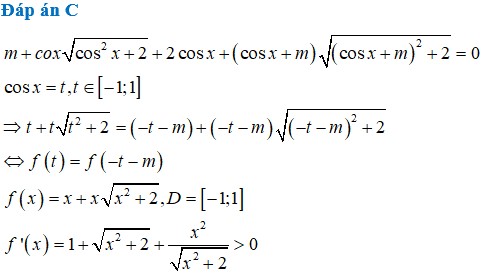Giá trị của m để phương trình cosx-m=0 vô nghiệm là ?

Những câu hỏi liên quan
Tất cả các giá trị của m để hương trình
cos
x
−
m
0
vô nghiệm là A.
−
1
≤
m
≤
1
B.
m
1
C.
m
−
1
m...
Đọc tiếp
Tất cả các giá trị của m để hương trình cos x − m = 0 vô nghiệm là
A. − 1 ≤ m ≤ 1
B. m > 1
C. m < − 1 m > 1
D. m < − 1
Đáp án là C
phương trình đã cho vô nghiệm khi m > 1
Đúng 0
Bình luận (0)
tìm tất cả các giá trị của m để phương trình \(\dfrac{sinx+2}{cosx}=m\) vô nghiệm
\(\Rightarrow sinx+2=m.cosx\)
\(\Rightarrow sinx-m.cosx=-2\)
Pt đã cho vô nghiệm khi:
\(1^2+\left(-m\right)^2< \left(-2\right)^2\)
\(\Rightarrow m^2< 3\)
\(\Rightarrow-\sqrt{3}< m< \sqrt{3}\)
Đúng 1
Bình luận (0)
Cho phương trình sinx.cosx - sinx - cosx + m 0, trong đó m là tham số thực. Để phương trình có nghiệm, các giá trị thích hợp của m là A.
-
2
≤
m
≤
-
1
2
-
2
B.
-
1
2
-
2
≤
m
≤
1
C.
1
≤...
Đọc tiếp
Cho phương trình sinx.cosx - sinx - cosx + m = 0, trong đó m là tham số thực. Để phương trình có nghiệm, các giá trị thích hợp của m là
A. - 2 ≤ m ≤ - 1 2 - 2
B. - 1 2 - 2 ≤ m ≤ 1
C. 1 ≤ m ≤ 1 2 + 2
D. 1 2 + 2 ≤ m ≤ 2
Có bao nhiêu giá trị nguyên của tham số m để phương trình
m
+
c
o
s
x
c
o
s
2
x
+
2
+
2
c
o
s
x
+
(
c
o
s
x
+
m
)
(
c
o...
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để phương trình m + c o s x c o s 2 x + 2 + 2 c o s x + ( c o s x + m ) ( c o s x + m ) 2 + 2 = 0 có nghiệm thực
A. 3
B. 4
C. 5
D. 6
Tất cả các giá trị của m để phương trình cos x – m 0 vô nghiệm là
Đọc tiếp
Tất cả các giá trị của m để phương trình cos x – m = 0 vô nghiệm là
![]()
![]()
![]()
Giá trị của m để phương trình (m - 1)
x
2
- (2m - 2)x + 2m 0 vô nghiệm là: A.
[
m
≥
2
m
-
2
B.
[
m
≥
3
m...
Đọc tiếp
Giá trị của m để phương trình (m - 1) x 2 - (2m - 2)x + 2m = 0 vô nghiệm là:
A. [ m ≥ 2 m < - 2
B. [ m ≥ 3 m < - 3
C. [ m ≥ 1 m < - 1
D. [ m ≥ 4 m < - 4
Chọn C.
Với m = 1 thỏa mãn yêu cầu bài toán
Với m ≠ 1 phương trình vô nghiệm khi và chỉ khi Δ' < 0
⇔ (m - 1 ) 2 - 2m(m - 1) < 0 ⇔ (m - 1)(-m - 1) < 0
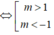
Vậy với 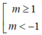 thì phương trình có nghiệm
thì phương trình có nghiệm
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị nguyên của tham số m để phương trình
sin
x
cos
x
−
sin
x
−
cos
x
+
m
0
có nghiệm? A. 1 B. 2 C. 3 D. 4
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để phương trình sin x cos x − sin x − cos x + m = 0 có nghiệm?
A. 1
B. 2
C. 3
D. 4
Đặt t = sin x + cos x − 2 ≤ t ≤ 2 ⇒ sin x cos x = t 2 − 1 2 .
Phương trình trở thành t 2 − 1 2 − t + m = 0 ⇔ − 2 m = t 2 − 2 t − 1 ⇔ t − 1 2 = − 2 m + 2 .
Do − 2 ≤ t ≤ 2 ⇒ − 2 − 1 ≤ t − 1 ≤ 2 − 1 ⇔ 0 ≤ t − 1 2 ≤ 3 + 2 2 .
Vậy để phương trình có nghiệm
⇔ 0 ≤ − 2 m + 2 ≤ 3 + 2 2 ⇔ − 1 + 2 2 2 ≤ m ≤ 1 → m ∈ ℤ m ∈ − 1 ; 0 ; 1 .
Chọn đáp án C.
Đúng 0
Bình luận (0)
Cho phương trình: x 4 - 13 x 2 + m = 0 . Tìm các giá trị của m để phương trình: Vô nghiệm
Phương trình (1) vô nghiệm khi phương trình (2) có 2 nghiệm số âm hoặc vô nghiệm.
Nếu phương trình (2) có 2 nghiệm âm thì theo hệ thức Vi-ét ta có:
t 1 + t 2 = 13 > 0 vô lý
Vậy phương trình (1) vô nghiệm khi phương trình (2) vô nghiệm.
Suy ra: ∆ = 169 - 4m < 0 ⇔ m > 169/4}
Đúng 0
Bình luận (0)
Giá trị của tham số m để phương trình ( 3 - m ) x - m 2 + 9 = 0 có vô số nghiệm là:
![]()
B. m > 3.
C. m < 3.
D. m = 3.
Đáp án: D
Để phương trình (3 – m )x – m 2 + 9 = 0 có vô số nghiệm thì
3 - m = 0 m 2 - 9 = 0 ⇔ m = 3
Đúng 0
Bình luận (0)
Cho phương trình ( m – 3 ) x 2 – 2 m x + m − 6 = 0 . Tìm các giá trị của m để phương trình vô nghiệm
A. m < −2
B. m < 2
C. m < 3
D. m < −3
Phương trình (m – 3)x2 – 2mx + m − 6 = 0
có a = m – 3; b’ = −m; c = m – 6
Suy ra Δ ' = (−m)2 – (m − 3)(m – 6) = 9m – 18
TH1: m – 3 = 0 ⇔ m = 3 −6x – 3 = 0
⇔ x = − 1 2
TH2: m – 3 ≠ 0 ⇔ m ≠ 3
Để phương trình vô nghiệm thì:
a ≠ 0 Δ ' < 0 ⇔ m ≠ 3 9 m − 18 < 0 ⇔ m ≠ 3 m < 2 ⇔ m < 2
Vậy m < 2 là giá trị cần tìm
Đáp án cần chọn là: B
Đúng 0
Bình luận (0)