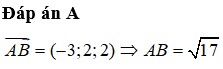1 rong ko gian Oxyz, cho hai điểm A (-2;3;0) , B (2;-1;2). Mặt cầu nhận AB là đường kính có pt là
2 rong ko gian với hệ tọa độ Oxyz , cho điểm M (1;2;3). Điểm N đối xứng với M qua mp ( Oxy) có tọa độ
3 rong ko gian Oxyz khoảng cách tử điểm M (3;-4;1) tới mặt phẳng Oyz bằng
4 Tìm tập nghiệm pt \(4^{x+\frac{1}{2}}-5.2^x+2=0\) là
5 Nếu một khối cầu có thể tích V =36\(\pi\) thì diện tích của mặt cầu đó bằng
6 Cho hàm bậc bốn có đô thị như hình vẽ, pt 2f(x)+5=0
7 Tổng phần thực và phần ảo của số phức z thỏa mãn iz+(1-i).\(\overline{z}\) =-2i
8 Tập nghiệm của bất pt \(log_2\left(3x-1\right)\le3\) là
9 Trong ko gian vói hệ tọa độ Oyxz d1\(\left\{{}\begin{matrix}x=1-2t\\y=3+4t\\z=-2+6t\end{matrix}\right.\) và d2 \(\left\{{}\begin{matrix}x=1-s\\y=2+2s\\z=3s\end{matrix}\right.\) khẳng định nào đúng
A d1//d2 B d1\(\equiv\) d2 C d1 và d2 chéo nhau D d1\(\perp\) d2
10 Cho (H) là hình phẳng giới hạn bởi đồ thị hàm số y= \(e^x\) trục Ox và hai đường thẳng x=0 và x=1 . Thể tích khối rọn xoay tạo thành khi quay(H) xung quanh trục Ox
11 Nếu \(\int_0^2f\left(x\right)dx=3\) và \(\int_0^5f\left(x\right)dx=6\) thì \(\int_2^5\) f(x) bằng
12 Gọi z là nghiệm phức có phần ảo âm của pt \(z ^2-4z+8=0\) . Tính /w/với w=(1-2i)z
13 Cho cấp số nhân (un) với u1=2 và công bội q=-3 . Số hạng u3 bằng
14 Cho hình trụ có tỉ số diện tích xung quanh và diện tich toàn phần bằng \(\frac{1}{3}\) . Biết thể tích khối trụ bằng 4\(\pi\). Bán kính đáy của hình trụ là
15 Gỉa sử hàm số y=f(x) liên tục trên R và \(\int_3^5f\left(x\right)dx=a\) . Tích phân I=\(\int_1^2f\left(2x+1\right)dx\) có giá trị là
16 Cho lăng trụ đứng ABCD \(A^,B^,C^,D^,\) Có đáy là hình vuông cạnh a , cạnh bên \(AA^,\) =\(\frac{a\sqrt{6}}{2}\) Góc giữa hai mp \(A^,BD\) VÀ \(C^,BD\)
17 ĐỒ thị hàm số y= x^3-3x^2+2ax+b có điểm cực tiểu A(2;-2) . Khi đó a+b là
18 Cho số phức z thỏa /z/ =3 . Biết rằng tập hợp các số phức w=\(\overline{z}\)+i là một dg tròn . Tìm tâm của đường tròn đó