Đáp án C
Đường thẳng AB đi qua điểm B(3;-5;2) và có vectơ chỉ phương là AB → . Vậy phương trình chính tắc của đường thẳng AB là:
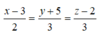
Đáp án C
Đường thẳng AB đi qua điểm B(3;-5;2) và có vectơ chỉ phương là AB → . Vậy phương trình chính tắc của đường thẳng AB là:
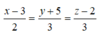
Trong không gian Oxyz, cho đường thẳng d là giao tuyến của hai mặt phẳng cắt nhau (P): x + y - z + 3 = 0, (Q): 2x - y + 6z - 2 = 0. phương trình chính tắc của đường thẳng d là:
A. x - 2 5 = y - 8 = z - 1 - 3
B. x + 2 5 = y - 8 = z - 1 - 3
C. x + 2 5 = y 8 = z - 1 - 3
D. x - 2 5 = y 8 = z - 1 - 3
Trong không gian Oxyz, cho hai điểm A(1; -2; 0), B(3; -5; 2). Phương trình tham số của đường thẳng AB là:
A. x - 3 2 = y + 5 - 3 = z - 2 2
B. x = 2 + 3t, y = -3 - 5t, z = 2 + 2t
C. x = 3 + 2t, y = -5 - 3t, z = 2 + 2t
D. x = 1 + 2t, y = -2 + 3t, z = 2t
Trong không gian Oxyz, cho đường thẳng d đi qua M(4;3;1) và song song với đường thẳng Δ: x = 1 + 2t, y = 1 - 3t, z = 3 + 2t. Phương trình chính tắc của đường thẳng d là:
A. x - 1 1 = y - 2 - 2 = z + 3 3
B. x - 1 - 1 = y + 2 - 2 = z - 3 3
C. x + 1 - 1 = y - 2 - 2 = z + 3 3
D. x + 1 - 1 = y + 2 - 2 = z - 3 3
Bài tập 6. Trong mặt phẳng Oxy, cho hai đường thẳng Delta_{1} / 2 * x - y - 2 = 0 , Delta_{2} / x - y + 3 = 0 và hai điểm A(-1;3) , B(0;2) . a. Viết phương trình đường thẳng qua AB. b. Viết phương trình đường thẳng trung trực của đoạn thẳng AB . c. Viết phương trình đường thẳng qua 4 và song song với Delta_{1} . d. Viết phương trình đường thẳng qua 4 và vuông góc với Delta_{1} e. Viết phương trình đường thẳng qua B và có hệ số góc k = - 3 . f. Tính côsin góc giữa hai đường thẳng Delta_{1}, Delta_{2} g. Tính d(A, Delta_{2}) . h. Viết phương trình đường thẳng qua 4 và tạo với Delta_{1} một góc c biết cos varphi = 1/(sqrt(5)) i. Tìm tọa độ hình chiếu vuông góc của 4 trên Delta_{2} j. Tìm tọa độ điểm B^ prime d hat oi xứng với B qua Delta_{2}
Trong không gian Oxyz, cho đường thẳng d: x = 1 + t, y = 2 -2t, z = -3. Viết phương trình tham số của đường thẳng Δ nằm trong mặt phẳng (Oxy), song song với d sao cho khoảng cách giữa hai đường thẳng d và Δ đạt giá trị nhỏ nhất
A. d: x = 1 + t, y = 2 -2t, z = 0
B. d: x = 1 + t, y = -2t, z = -3
C. d: x = t, y = 2 - 2t, z = -3
D. d: x = 1, y = 2, z = -3 + t
Bài 1. Viết phương trình tổng quát, phương trình tham số của đường thẳng trong mỗi trường hợp sau:
a) Đi qua A(1;-2) và // với đường thẳng 2x - 3y - 3 = 0.
b) Đi qua hai điểm M(1;-1) và N(3;2).
c) Đi qua điểm P(2;1) và vuông góc với đường thẳng x - y + 5 = 0.
Bài 2. Cho tam giác ABC biết A(-4;1), B(2;4), C(2;-2).
Tính khoảng cách từ điểm C đến đường thẳng AB.
Bài 3. Cho tam giaùc ABC coù: A(3;-5), B(1;-3), C(2;-2).Vieát phöông trình toång quaùt cuûa:
a) 3 caïnh AB, AC, BC
b) Ñöôøng thaúng qua A vaø song song vôùi BC
c)Trung tuyeán AM vaø ñöôøng cao AH cuûa tam giaùc ABC
d) Ñöôøng thaúng qua troïng taâm G cuûa tam giaùc ABC vaø vuoâng goùc vôùi AC
e) Ñöôøng trung tröïc cuûa caïnh BC
Bài 4. Cho tam giaùc ABC coù: A(1 ; 3), B(5 ; 6), C(7 ; 0).:
a) Vieát phöông trình toång quaùt cuûa 3 caïnh AB, AC, BC
b) Viết phương trình đđöôøng trung bình song song cạnh AB
c) Viết phương trình đường thẳng qua A và cắt hai trục tọa độ tại M,N sao cho AM = AN
d) Tìm tọa độ điểm A’ là chân đường cao kẻ từ A trong tam giaùc ABC
Bài 5. Viết phương trình đường tròn có tâm I(1; -2) và
a) đi qua điểm A(3;5).
b) tiếp xúc với đường thẳng có pt x + y = 1.
Trong không gian Oxyz, cho mặt cầu (S) có phương trình là: ( x + 1 ) 2 + ( y - 4 ) 2 + ( z + 3 ) 2 = 36. Số mặt phẳng (P) chứa trục Ox và tiếp xúc với mặt cầu (S) là:
A. 0
B. 1
C. 2
D. Vô số
Trong không gian Oxyz, lập phương trình tham số của đường thẳng d là giao tuyến của hai mặt phẳng cắt nhau: (P): x + 2y - z + 1 = 0, (Q): x + y + 2z + 3 = 0
A. d: x = -5 - 5t, y = 2 + 3t, z = t
B. d: x = -5 - 5t, y = 2 - 3t, z = t
C. d: x = -5 + 5t, y = 2 + 3t, z = t
D. d: x = 5t, y = 3 - 3t, z = -t
Nghiệm của hệ phương trình sau là:
![]()
A. x = 2, y = -3 B. x = -2, y = 3
C. x = -1, y = -2 D. x = 1, y = 5