Cho ΔABC có 3 góc nhọn. Kẻ các đường cao AD,BE,CF chúng cắt nhau tại H. Chứng minh rằng:
a) ΔAEB∽ΔAFC
b) AD. HB = AB . DF
c) DA là phân giác của EDF
Những câu hỏi liên quan
Cho tam giác nhọn ABC, các đường cao AD, BE, CF cắt nhau tại H.a) Chứng minh ΔAEB và ΔAFC đồng dạng. Từ đó suy ra:
A
F
.
A
B
A
E
.
A
C
b) Chứng minh
∠
A
E
F
∠
A
B
C
c) Cho
A
E
3
c
m
,...
Đọc tiếp
Cho tam giác nhọn ABC, các đường cao AD, BE, CF cắt nhau tại H.
a) Chứng minh ΔAEB và ΔAFC đồng dạng. Từ đó suy ra: A F . A B = A E . A C
b) Chứng minh ∠ A E F = ∠ A B C
c) Cho A E = 3 c m , A B = 6 c m . Chứng minh rằng S A B C = 4 S A E F
d) Chứng minh A F F B . B D D C . C E E A = 1
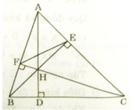
a) Xét ΔAEB và ΔAFC có:
∠AEB = ∠AFC = 90o (gt)
∠A chung
Vậy ΔAEB ∼ ΔAFC (g.g)
b) Xét ΔAEF và ΔABC có
∠A chung
AF.AB = AE.AC (Cmt)
⇒ ΔAEF ∼ ΔABC (c.g.c)
⇒ ∠AEF = ∠ABC
c) ΔAEF ∼ ΔABC (cmt)
Đúng 4
Bình luận (0)
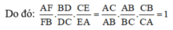
Cho tam giác ABC có 3 goc nhọn. Kẻ các đường cao AD, BE, CF cắt nhau tại H a/ Chứng minh tứ giác BDHF, ACDF, CFHD, ABDE nội tiếp b/ chứng minh DH là tia phân giác của EDF
a: Xét tứ giác BDHF có \(\widehat{BDH}+\widehat{BFH}=90^0+90^0=180^0\)
=>BDHF là tứ giác nội tiếp
Xét tứ giác AFDC có \(\widehat{AFC}=\widehat{ADC}=90^0\)
nên AFDC là tứ giác nội tiếp
Sửa đề; CEHD
Xét tứ giác CEHD có
\(\widehat{CEH}+\widehat{CDH}=90^0+90^0=180^0\)
=>CEHD là tứ giác nội tiếp
Xét tứ giác ABDE có \(\widehat{AEB}=\widehat{ADB}=90^0\)
nên ABDE là tứ giác nội tiếp
b: Ta có: \(\widehat{FDH}=\widehat{FBH}\)(FBDH là tứ giác nội tiếp)
\(\widehat{EDH}=\widehat{ECH}\)(ECDH là tứ giác nội tiếp)
mà \(\widehat{FBH}=\widehat{ECH}\left(=90^0-\widehat{FAC}\right)\)
nên \(\widehat{FDH}=\widehat{EDH}\)
=>DH là phân giác của góc EDF
Đúng 0
Bình luận (0)
Cho ΔABC nhọn, ba đường cao AD, BE, CF cắt nhau tại H. Chứng minh rằng:
a) EH.HB = DH.HA
b) ΔEHD ~ ΔAHB.
c) ΔFHD ~ ΔAHC.
d) DH là tia phân giác của góc EDF.
cho tam giác abc có 3 góc nhọn đường cao ad be cf cắt nhau tại h
a) chứng minh ae*ac-af*ab từ đó suy ra tam giác abc đồng dạng tam giác aef
b) chứng minh ah*dh=bh*eh=ch*fh
c) chứng minh da là tia phân giác của góc edf
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O).Ba đường cao AD,BE,CF cắt nhau tại H (D Thuộc BC, E thuộc AC, F Thuộc AB )
a) Chứng minh tứ giác BFHD là tứ giác nội tiếp.
b) Chứng minh BF.Ba=BD.BC
c) Chứng minh DA là tia phân giác của góc EDF
Cho tam giác ABC có ba góc nhọn, AB AC. Kẻ đường cao AD. Vẽ điểm M sao cho AB là trung trực của DM, vẽ điểm N sao cho AC là trung trực của DN.a) Chứng minh tam giác AMN cân tại Ab) Đường thẳng MN cắt AB, AC lần lượt tại F, E. Chứng minh DA là tia phân giác của
E
D
F
^
.c) Chứng minh EB là tia phân giác của
D
E
F
^...
Đọc tiếp
Cho tam giác ABC có ba góc nhọn, AB < AC. Kẻ đường cao AD. Vẽ điểm M sao cho AB là trung trực của DM, vẽ điểm N sao cho AC là trung trực của DN.
a) Chứng minh tam giác AMN cân tại A
b) Đường thẳng MN cắt AB, AC lần lượt tại F, E. Chứng minh DA là tia phân giác của E D F ^ .
c) Chứng minh EB là tia phân giác của D E F ^ .
d) Chứng minh B E ⊥ A C .
e) Chứng minh AD, BE, CF đồng quy.
cho tam giác ABC, có ba góc nhọn, AB<AC. kẻ các đường cao AD,BE,CF cắt nhau tại H.
a) chứng minh: góc BAD bằng góc FEB
b) chứng minh: DA là phân giác của góc EDF, từ đó suy ra H cách đều EF,FD, ED
c) gọi S là giao điểm AD vả EF, chứng minh:tích của SH và AD bằng tích của AS và HD
d) gọi J,M lần lượt là trung điểm AH, BH , chứng minh JE,MD cùng cách đều một điểm
Cho ΔABC có AB = AC, tia phân giác của góc BAC cắt BC tại D.
1) Chứng minh rằng: AD ⊥ BC .
2) Lấy điểm E thuộc AB, điểm F thuộc AC, sao cho BE = CF. Chứng minh DA là tia phân giác của góc EDF.
1: Xét ΔADB và ΔADC có
AB=AC
\(\widehat{BAD}=\widehat{CAD}\)
AD chung
Do đó: ΔADB=ΔADC
=>\(\widehat{ADB}=\widehat{ADC}\)
mà \(\widehat{ADB}+\widehat{ADC}=180^0\)(hai góc kề bù)
nên \(\widehat{ADB}=\widehat{ADC}=\dfrac{180^0}{2}=90^0\)
=>AD\(\perp\)BC
2: Ta có: AE+EB=AB
AF+FC=AC
mà EB=FC và AB=AC
nên AE=AF
Xét ΔEAD và ΔFAD có
AE=AF
\(\widehat{EAD}=\widehat{FAD}\)
AD chung
Do đó: ΔEAD=ΔFAD
=>\(\widehat{EDA}=\widehat{FDA}\)
=>DA là phân giác của góc EDF
Đúng 2
Bình luận (0)
Lời giải:
1. Xét tam giác $ABD$ và $ACD$ có:
$AB=AC$
$\widehat{BAD}=\widehat{CAD}$ (do $AD$ là tia phân giác $\widehat{BAC}$)
$AD$ chung
$\Rightarrow \triangle BAD=\triangle CAD$ (c.g.c)
$\Rightarrow \widehat{ADB}=\widehat{ADC}$
Mà $\widehat{ADB}+\widehat{ADC}=180^0$
$\Rightarrow \widehat{ADB}=\widehat{ADC}=180^0:2=90^0$
$\Rightarrow AD\perp BC$
2.
$AB=AC$
$BE=CF$
$\Rightarrow AB-BE=AC-CF$ hay $AE=AF$
Xét tam giác $AED$ và $AFD$ có:
$AD$ chung
$AE=AF$
$\widehat{EAD}=\widehat{FAD}$
$\Rightarrow \triangle AED=\triangle AFD$ (c.g.c)
$\Rightarrow \widehat{EDA}=\widehat{FDA}$
$\Rightarrow DA$ là tia phân giác $\widehat{EDF}$
Đúng 2
Bình luận (0)
Cho tam giác ABC nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cát nhau tại H.
a) Chứng minh các tứ giác BFEC, BFHD nội tiếp
b) Chứng minh DH là tia phân giác của góc EDF
c) Kẻ AD cát chungBC tại M. Chứng minh tam giác BMH cân