Cho hình bình hành ABCDcó tâm o chứng minh rằng AO-OB

Những câu hỏi liên quan
Câu 1:cho hình bình hành ABCD tâm O chứng minh BD-BA=OC-OB và BC-BD+BA=O
Câu 2: cho hình bình hành ABCD tâm O. m là điểm tuỳ ý chứng minh AB+OA=OB và MA+MC=MB+MD
Xem chi tiết
Câu 1: giả sử:\(\overrightarrow{BD}-\overrightarrow{BA}=\overrightarrow{OC}-\overrightarrow{OB}\Leftrightarrow\overrightarrow{BA}+\overrightarrow{AD}-\overrightarrow{BA}=\overrightarrow{OC}+\overrightarrow{BO}\)
\(\Leftrightarrow\overrightarrow{AD}=\overrightarrow{BC}\)(luôn đúng vì ABCD lad hình bình hành)
giả sử: \(\overrightarrow{BC}-\overrightarrow{BD}+\overrightarrow{BA}=\overrightarrow{0}\Leftrightarrow\overrightarrow{BC}-\overrightarrow{BC}+\overrightarrow{DC}+\overrightarrow{BA}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{BB}+\overrightarrow{DD}=\overrightarrow{0}\)(LUÔN ĐÚNG)
câu 2 :GIẢ SỬ:
\(\overrightarrow{AB}+\overrightarrow{OA}=\overrightarrow{OB}\Leftrightarrow\overrightarrow{AO}+\overrightarrow{OB}+\overrightarrow{OA}+\overrightarrow{BO}=\overrightarrow{0}\)(luôn đúng)
giả sử: \(\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{MB}+\overrightarrow{MD}\\ \Leftrightarrow\overrightarrow{MB}+\overrightarrow{BA}+\overrightarrow{MD}+\overrightarrow{DC}=\overrightarrow{MB}+\overrightarrow{MD}\Leftrightarrow\overrightarrow{0}=\overrightarrow{0}\)
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD, O là giao điểm của hai đường chéo. Gọi M, N lần lượt là trung điểm OB, OD
a) Chứng minh AMCN là hình bình hành
b) Hình bình hành ABCD cần có thêm điều kiện gì để AMCN là hình chữ nhật
c) AN cắt CD tại E, CM cắt AB tại tâm O. Chứng minh rằng E và F đối xứng với nhau qua tâm O
Cho hình bình hành ABCD tâm O chứng minh các vecto BD-BA=OC-OB Giúp mình với ạ
\(\overrightarrow{OC}-\overrightarrow{OB}=\overrightarrow{BO}+\overrightarrow{OC}=\overrightarrow{BC}\)(1)
ABCD là hình bình hành
=>\(\overrightarrow{BD}=\overrightarrow{BA}+\overrightarrow{BC}\)
=>\(\overrightarrow{BC}=\overrightarrow{BD}-\overrightarrow{BA}\left(2\right)\)
Từ (1) và (2) suy ra \(\overrightarrow{OC}-\overrightarrow{OB}=\overrightarrow{BD}-\overrightarrow{BA}\)
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD có tâm O. Chứng minh rằng:
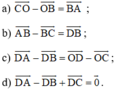
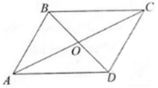
a) Ta có:
O là trung điểm của AC nên 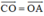
Do đó 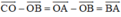
b) ABCD là hình bình hành nên 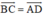
Do đó 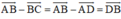
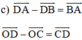
Mà ABCD là hình bình hành nên 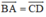
Do đó 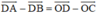
d) ABCD là hình bình hành nên 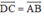
Lại có 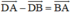
Do đó 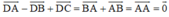
Đúng 0
Bình luận (0)
Cho tâm giác ABC vuông tại A,M là trung điểm của BC.Gọi K và N lần lượt là chân đường vuông gốc từ M đến AB và AC a) Chứng minh AKMN là hình chứ nhật b)Chứng minh NKMC là hình bình hành c) gọi O là điểm đối xứng của N qua M chứng minh rằng AO,BN,CK đồng quy
Vì △ABC vuông tại A (gt)
=> AB ⊥ AC
=> góc BAC = 90 độ
mà K ∈ AB; N ∈ AC
=> góc KAN = 90 độ
Xét tứ giác AKMN có :
góc MKA = 90 độ (MK ⊥ AB mà K ∈ AB)
góc KAN = 90 độ (cmt)
góc ANM = 90 độ (MN ⊥ ACmà N ∈ AC)
=> AKMN là hình chữ nhật (DHNB)
b) Vì AKMN là hình chữ nhật (cmt)
=> MN // AK mà K ∈ AB
=> MN // AB
Xét △ABC có : M là trung điểm BC (gt)
MN // AB (cmt)
=> N là trung điểm AC
=> NA = NC
mà NA = KM (vì AKMN là hình chữ nhật)
=> NC = KM
Xét tứ giác NKMC có : NC // KM ( KM // AN mà N ∈ AC)
NC = KM (cmt)
=> NKMC là hình bình hành (DHNB)
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD có hai đường chéo AC và BD cắt nhau tại O. Gọi M, N, P, Q lần lượt là trung điểm các đoạn OA, OB, OC, OD
1) Chứng minh rằng tứ giác MNPQ là hình bình hành
2) Chứng minh rằng các tứ giác ANCQ, BPDM là các hình bình hành
1) Vì ABCD là hình bình hành
=> OA=OC, OB=OD
Ta có: OM=OA/2
OP=OC/2
Mà OA=OC => OM=OP
Cm tương tự ta được OQ=ON
Tứ giác MNPQ có OM=OP. OQ=ON
=> MNPQ là hình bình hành
2) Tứ giác ANCQ có OA=OC (cmt), OQ=ON (cmt)
Suy ra tứ giác ANCQ là hình bình hành
Tứ giác BPDM có OB=OD (cmt), OM=OP (cmt)
Suy ra tứ giác BPDM là hình bình hành
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD có tâm (giao hai đường chéo) là O.a) Chứng minh rằng mỗi đường thẳng d đi qua O đều chia hình bình hành thành haiphần có chu vi bằng nhau và diện tích bằng nhau.b) Một đường thẳng d chia hình bình hành thành hai phần có diện tích bằng nhau,chứng minh rằng nó đi qua O.c) Một đường thẳng d chia hình bình hành thành hai phần có chu vi bằng nhau, chứngminh rằng nó đi qua O.
Đọc tiếp
Cho hình bình hành ABCD có tâm (giao hai đường chéo) là O.
a) Chứng minh rằng mỗi đường thẳng d đi qua O đều chia hình bình hành thành hai
phần có chu vi bằng nhau và diện tích bằng nhau.
b) Một đường thẳng d chia hình bình hành thành hai phần có diện tích bằng nhau,
chứng minh rằng nó đi qua O.
c) Một đường thẳng d chia hình bình hành thành hai phần có chu vi bằng nhau, chứng
minh rằng nó đi qua O.
Cho hình bình hành MNPQ có các đỉnh M, N, P, Q laanf lượt nằm trên các cạnh AB, BC, CD, DA của hình bình hành ABCD
Chứng minh rằng hai hình bình hành đó có cùng tâm O.
Cho hình bình hành ABCD tâm O. Chứng minh OA+OB+OC+OD= véctơ 0



















